General matrix representation of lorentz boost

[highwaychile]

Hello!

I'm trying to derive the general matrix form of a lorentz boost by using the generators of rotations and boosts:

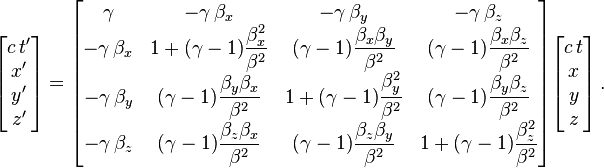
I already managed to get the matrices that represent boosts in the direction of one axis, but when trying to combine them to get a boost in an arbitrary direction I always fail; my first try was to execute the three boosts after each other, but of course this did not work :)

Then I found this thread where I learned that I've to rotate, then do a boost, and afterwards undo the rotation; but unfortunately it does not work :(

Here is what I do (I also attached my mathematica notebook):

1. Initialize the generators of rotation (s) / boosts (k):

s1 = {{0, 0, 0, 0}, {0, 0, 0, 0}, {0, 0, 0, -1}, {0, 0, 1, 0}};
s2 = {{0, 0, 0, 0}, {0, 0, 0, 1}, {0, 0, 0, 0}, {0, -1, 0, 0}};
s3 = {{0, 0, 0, 0}, {0, 0, -1, 0}, {0, 1, 0, 0}, {0, 0, 0, 0}};
k1 = {{0, 1, 0, 0}, {1, 0, 0, 0}, {0, 0, 0, 0}, {0, 0, 0, 0}};
k2 = {{0, 0, 1, 0}, {0, 0, 0, 0}, {1, 0, 0, 0}, {0, 0, 0, 0}};
k3 = {{0, 0, 0, 1}, {0, 0, 0, 0}, {0, 0, 0, 0}, {1, 0, 0, 0}};
Rot[m_, ω_] := MatrixExp[-ω*m];
Boost[m_, ζ_] := MatrixExp[-ζ*m];

2. Generate a boost in x direction:

boostX = Boost[k1, x];

3. To get a boost in y direction, I rotate around the z-axis by pi/2, then boost to x axis, then undo the rotation:

boostY = Rot[s3, -\[Pi]/2].Boost[k1, y].Rot[s3, \[Pi]/2];

4. To get a boost in z direction I do the same as above, but this time I'm rotating around the y axis:

boostZ = Rot[s2, -\[Pi]/2].Boost[k1, z].Rot[s2, \[Pi]/2];

5. Now I'm combining the boosts:

Simplify[boostX.boostY.boostZ] // MatrixForm
[itex]\left(
\begin{array}{cccc}
\frac{1}{8} e^{-x-y-z} \left(1+e^{2 x}\right) \left(1+e^{2 y}\right) \left(1+e^{2 z}\right) & -\frac{1}{2} e^{-x} \left(-1+e^{2 x}\right) & -\frac{1}{4} e^{-x-y} \left(1+e^{2 x}\right) \left(-1+e^{2 y}\right) & \frac{1}{8} e^{-x-y-z} \left(1+e^{2 x}\right) \left(1+e^{2 y}\right) \left(-1+e^{2 z}\right) \\
-\frac{1}{8} e^{-x-y-z} \left(-1+e^{2 x}\right) \left(1+e^{2 y}\right) \left(1+e^{2 z}\right) & \frac{1}{2} e^{-x} \left(1+e^{2 x}\right) & \frac{1}{4} e^{-x-y} \left(-1+e^{2 x}\right) \left(-1+e^{2 y}\right) & -\frac{1}{8} e^{-x-y-z} \left(-1+e^{2 x}\right) \left(1+e^{2 y}\right) \left(-1+e^{2 z}\right) \\
-\frac{1}{4} e^{-y-z} \left(-1+e^{2 y}\right) \left(1+e^{2 z}\right) & 0 & \frac{1}{2} e^{-y} \left(1+e^{2 y}\right) & -\frac{1}{4} e^{-y-z} \left(-1+e^{2 y}\right) \left(-1+e^{2 z}\right) \\
\frac{1}{2} e^{-z} \left(-1+e^{2 z}\right) & 0 & 0 & \frac{1}{2} e^{-z} \left(1+e^{2 z}\right) \\
\end{array}
\right)[/itex]

This result is clearly wrong as my matrix has elements that are 0 :(

I've been searching a lot what's the reason for this, but unfortunately I found no book explaining how to obtain the transformation matrix (e.g. Jackson electrodynamics leaves this as an exercise to the reader...) Can you help me, do you know what I'm doing wrong?

Thank you a lot in advance!

highwaychile

 

[Bill_K]

highwaychile, I'm afraid you're expending a great deal of effort trying to derive something that is instantly obvious by inspection! Does not need a lengthy derivation, and certainly does not need Mathematica.

Just look at the Lorentz matrix for a boost in the x direction:

$$\left(\begin{array}{cccc}\gamma&-\gamma\beta&0&0\\-\gamma\beta&\gamma&0&0\\0&0&1&0\\0&0&0&1\end{array}\right)$$

Let β be a 3-vector in the boost direction, and let n = β/β be the unit 3-vector in that same direction.

Look at the first row. The 00 component is just γ. The three 0i components form a 3-vector, -γβ. Now look at the first column. Again the i0 components form the same 3-vector, -γβ.

Finally, what's the 3x3 matrix of ij components? It's I + (γ-1)nn. Put these three pieces together and presto, you have the Lorentz matrix for a general boost.

 

[highwaychile]

you're right, that's a really simple solution, thank you!