DavidZuccaro
- 15
- 0
I herewith submit for reference, review and comment the general solution to 3 simultaneous equations as follows:
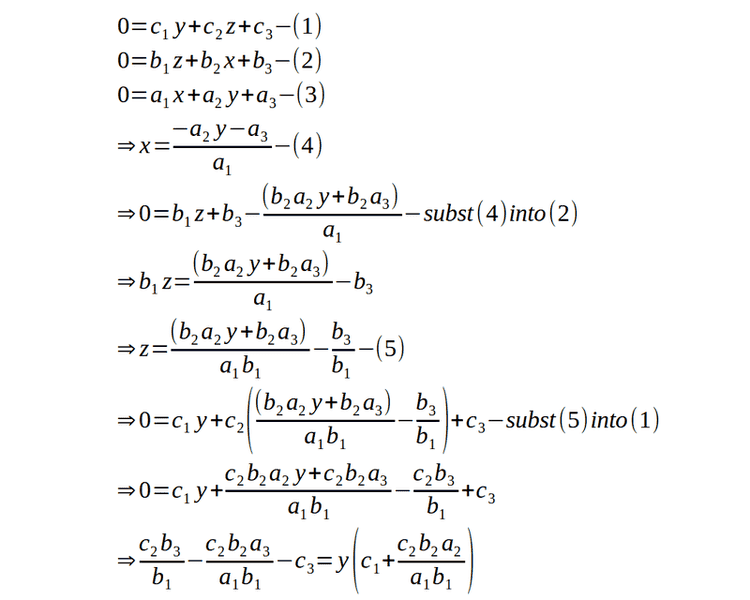
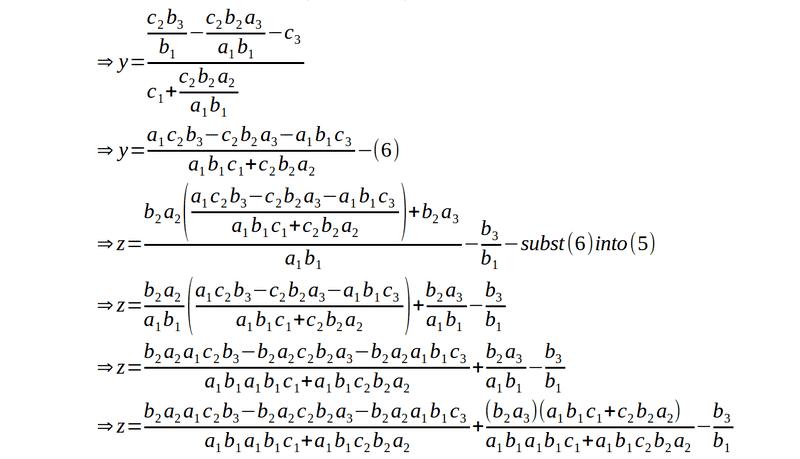
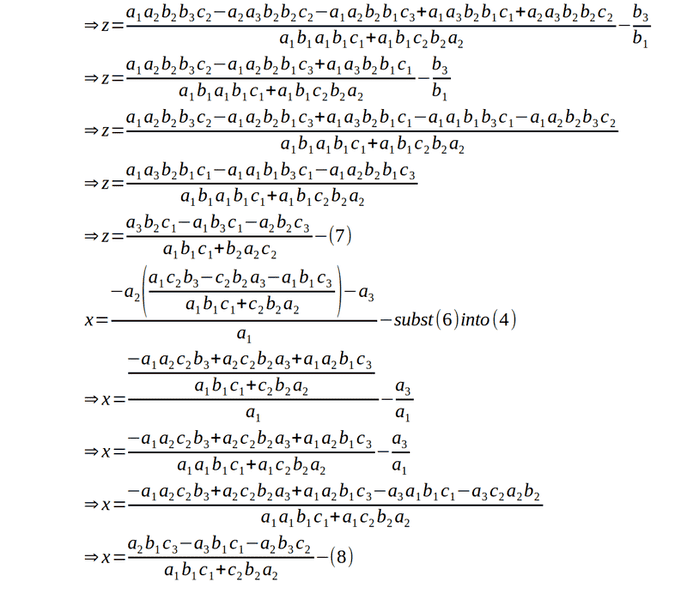
BvU said:Lot of work plus a lot of typesetting !
I do notice that you have written down a general solution for a not so general set of three equations in three unknowns.
Are you familiar with things like inverting a 3x3 matrix? Your matrix has zeros on the diagonal.