General Theory of Relativity: What & Why

[kaushikquanta]

what general theory of relativity deals with. why special theory of relativity fails at one stage

 

[martinbn]

Gravity

 

[klen]

what general theory of relativity deals with. why special theory of relativity fails at one stage

Special Theory of relativity deals with "special" kind of reference frames which are moving at constant velocities with respect to each other and where Galilean principle that free bodies move with constant velocity holds. Such special frames are the inertial frames i.e, where this law of inertia holds.
Einstein wanted that the physical laws should not depend on the frame of reference and laws of physics should be valid in "all" the frames even those which are accelerated with respect to the inertial frames. Thus general relativity frees the physical laws from the shackles of reference frames and presents a view of the physical world where the laws of physics can be described for any "general" frame.
It is not that special relativity fails at one stage but just that it only deals with special situation where the frames have to be inertial.

 

[Nugatory]

Special Theory of relativity deals with "special" kind of reference frames which are moving at constant velocities with respect to each other and where Galilean principle that free bodies move with constant velocity holds. Such special frames are the inertial frames i.e, where this law of inertia holds.

This is not right. The special theory works just fine for accelerations and in non-inertial frames (google for "Rindler coordinates" for one example) as long as we're working with a flat spacetime, which is to say no gravity.

General relativity is only needed when gravity is present so Martinbn's answer above ("gravity") is correct. What makes special relativity "special" is that it applies only to the special case of gravity-free flat spacetime, whereas general relativity is "general" because it works in the general case where gravity may be present. If you start with the equations of general relativity and set the gravitational effects to zero, you'll end up with special relativity.

 

[klen]

This is not right. The special theory works just fine for accelerations and in non-inertial frames (google for "Rindler coordinates" for one example) as long as we're working with a flat spacetime, which is to say no gravity.

I think special relativity is valid where Minkowskian distance in spacetime is invariant between various frames of reference. This is not the case with the accelerated frames where, as you said, distance is measured with different metric.

 

[Nugatory]

This is not the case with the accelerated frames where, as you said, distance is measured with different metric.

That is simply not true. The metric tensor is a property of the spacetime, not the frame that you use to assign coordinates to points in spacetime, so it is not different in accelerated frames. We're just writing it down using different coordinates so it looks different.

For an easier example, we could consider vectors in two-dimensional Euclidean space: If I define $u=x-y$ and $v=x+y$ then I can write the components of a particular vector as either $(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}$) using the x,y coordinate system or as $(1,0)$ using the u,v coordinate system. The two forms look completely different, and if you aren't aware of the relationship between the two sets of coordinates, it would be easy to think we're talking about different vectors - but it's the same vector, length one and slanting at a 45-degree angle up and right from the origin.

Like I said above... Check out Rindler coordinates... They're defined by a coordinate transformation that's more complicated than the simple (x,y) to (u,v) example above, but it's still just a coordinate transformation. We're attaching different labels to the points in spacetime, but it's the same spacetime.

 

[klen]

That is simply not true. The metric tensor is a property of the spacetime, not the frame that you use to assign coordinates to points in spacetime, so it is not different in accelerated frames. We're just writing it down using different coordinates so it looks different.

In Minkowskian space distance is measured by:

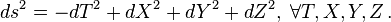
In Rindler coordinates it changes to:

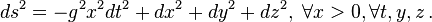
What I am saying is we cannot use the Minkowskian formula to calculate the distances in an accelerated frame. Special relativity holds only for the frames in which the above Minkowskian distance is invariant.

 

[stevendaryl]

In Minkowskian space distance is measured by:

In Rindler coordinates it changes to:

What I am saying is we cannot use the Minkowskian formula to calculate the distances in an accelerated frame. Special relativity holds only for the frames in which the above Minkowskian distance is invariant.

This is a quite common way of thinking about it, but I think it's not correct. Let me give you an analogy:

Newton's equations of motion in the absence of forces can be written as follows: (2 dimensions for simplicity)

m \frac{d^2 x}{dt^2} = 0
m \frac{d^2 y}{dt^2} = 0

However, if you switch from rectangular coordinates to polar coordinates r, \theta, then the equations of motion become:

m \frac{d^2 r}{dt^2} - m r (\frac{d\theta}{dt})^2 = 0
m r \frac{d^2 \theta}{dt^2} + 2 m \frac{dr}{dt} \frac{d\theta}{dt} = 0

The equations are different. But would anyone say that Newton's equations don't apply if you use polar coordinates? I don't think so. Instead, you just have to work what the equations of motion look like in polar coordinates.

 

[Smattering]

What I am saying is we cannot use the Minkowskian formula to calculate the distances in an accelerated frame. Special relativity holds only for the frames in which the above Minkowskian distance is invariant.

According to a radio feature I heard this morning, Einstein was sitting in some waiting room when he suddenly had the idea that someone who is in free fall will not feel his own weight. They quoted Einstein as saying that this was the key insight that inpired him to work on general relativity.

At least to me, this makes only sense if Einstein already had an idea how to handle accelarated frames. Because in that case, the equivalence between gravity and accelaration would allow him to reduce gravity to something that he already knew. If accelarated frames had been equally unwieldily to him as gravity, then the equivalence between them would not have led to any major insight.

 

[stevendaryl]

According to a radio feature I heard this morning, Einstein was sitting in some waiting room when he suddenly had the idea that someone who is in free fall will not feel his own weight. They quoted Einstein as saying that this was the key insight that inpired him to work on general relativity.

At least to me, this makes only sense if Einstein already had an idea how to handle accelarated frames. Because in that case, the equivalence between gravity and accelaration would allow him to reduce gravity to something that he already knew. If accelarated frames had been equally unwieldily to him as gravity, then the equivalence between them would not have led to any major insight.

That's exactly right. You don't need any extra theory to know what SR looks like in an accelerated frame, you just need calculus. If you know the equations of motion in good old intertial coordinates, then calculus will allow you to compute what they are in an accelerated coordinate system. What's special about General Relativity, compared to Newton's mechanics or Special Relativity, is that the equations look exactly the same, no matter what coordinate system you use, while the equations of NM or SR look very ugly in any frame other than an inertial frame. But it is perfectly possible to work with ugly equations.

 

[klen]

At least to me, this makes only sense if Einstein already had an idea how to handle accelarated frames. Because in that case, the equivalence between gravity and accelaration would allow him to reduce gravity to something that he already knew. If accelarated frames had been equally unwieldily to him as gravity, then the equivalence between them would not have led to any major insight.

Einstein's idea of Equivalence Principle was that freely falling reference frames can be "locally" considered inertial, which he knew how to deal with using SR. Based on this idea, Einstein argued what would happen in a gravitational field. And then found that accelerated frames could also be dealt with in a similar way (to that of gravity) locally.