Generalisations of area between two curves

[Gary Smart]

Homework Statement

The problem consists of investigating the area between two functions of the forms (Parabolic segment):
: y = mx + c and y = ax^2 + bx + c

The investigation involves finding a combination that has one of each of the above functions and finding an area of one. The area between the functions has to be in the first quarter (positive x and y).

2. The attempt at a solution
My investigation up to now has found the following:
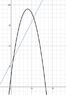
Function 1: 6x^2 - 2x + 8
Function 2: 4x + 8

These give points of intersection of: (0,8) and (1,12). These are the lower and upper bounds when integrating.

Integration produces:

Curve: 3x^2 - x^2 + 8x [Boundaries of 0 and 1]: Area under curve = 9 (between 0 and 1).

Line: 2x^2 + 8x [Boundaries of 0 and 1]; Area under line = 10 (Between 0 and 1).

=> Area between line and curve is: 10 - 9 = 1

3. Further investigations
I have already found that the coefficient of A (Parabola) has to be a multiple of 3, otherwise there will be a recurring decimal when integrated.

My next steps involve:
: Producing any generalisations that affect finding this specific area with these two functions.
: Proving/generalising using Algebra.

 

[LCKurtz]

There are a lot of things you haven't specified about this problem. May the parabola open either upwards or downwards? Must the intersections of the parabola and line be in the first quadrant? Is the area you want to calculate the area bounded by the two functions between the intersection points? Must the complete region "between" the functions lie in the first quadrant?

Also please show us how you got A must be a multiple of 3.

[Edit, added]: I would suggest starting with a simple subcase. For example, consider the two functions $(x-a)^2$ and $mx$. See if you can show that for any $a\ge 0$ there is a corresponding $m$ that works. Get the relationship between $m$ and $a$. Then start on more complicated cases.

 

[Gary Smart]

The Parabola can open either upwards or downwards. The intersections of the parabola and the line must be in the first quarter. The area is bounded by the functions between the points and the complete region between the functions must lie in the first quadrant.

I got that A must be a multiple of 3 because when the quadratic is integrated, the A value is divided by 3. If the value of A isn't a multiple of 3 then the result will always give a recurring decimal and will never produce an area of one.

(x-a)^2 = x^2 − 2xa + a^2 is not a parabola though is it?

 

[LCKurtz]

The Parabola can open either upwards or downwards. The intersections of the parabola and the line must be in the first quarter. The area is bounded by the functions between the points and the complete region between the functions must lie in the first quadrant.

I got that A must be a multiple of 3 because when the quadratic is integrated, the A value is divided by 3. If the value of A isn't a multiple of 3 then the result will always give a recurring decimal and will never produce an area of one.

(x-a)^2 = x^2 − 2xa + a^2 is not a parabola though is it?

That is a parabolic function. The graph of $y= (x-a)^2$ is a parabola with vertex $(a,0)$ opening upwards. $A$ does not have to equal $3$. Like I suggested, start with a real simple case. Take $y=(x-1)^2$ and $y = mx$. It is obvious geometrically that there is some positive $m$ so that the area between the line and parabola is $1$.

 

[Gary Smart]

Hello LCKurtz,

I not hundred percent sure I understand the process here. I have tried different m values when y = (x-1)^2 and it produces an m of approximately 0.704 (3 dp). What is the aim of the investigation?

 

[theodoros.mihos]

May you can use the absolute value of $$ \int_0^1f_1(x)dx-\int_0^1f_2(x) $$

 

[Gary Smart]

The first function being the line and the second function being the parabola?

 

[theodoros.mihos]

If you need just area, take absolute value. If you need sign then check for this on initial problem.

 

[Gary Smart]

Just to check I understand what you are saying:
I only need the area: specifically an area of 1 and if there are any generalisations that can be made.

What is the absolute value?

 

[theodoros.mihos]

Integral $\int f\,dx$ comes from area calculation between function graph and x axis.

 

[Gary Smart]

Integral $\int f\,dx$ comes from area calculation between function graph and x axis.

So, using that information.
The area of the function that is furthest away from the x-axis can't be less than 1?

 

[theodoros.mihos]

The integral have sign from f(x). The geometrical area is positive defined, like as geometrical distance. For area take the positive answer.

 

[Gary Smart]

The integral have sign from f(x). The geometrical area is positive defined, like as geometrical distance. For area take the positive answer.

This is because the area between the curves is above the x-axis and the fact there is no such thing as a negative geometrical distance?

 

[theodoros.mihos]

Area is positive, integral may not. Distance is positive, position coordinate value may not.

 

[Gary Smart]

Area is positive, integral may not. Distance is positive, position coordinate value may not.

I can't have negative integrals though? because the area is bounded in the first quadrant?

 

[theodoros.mihos]

Your parabola is positive defined so every $\int_a^bf_1(x)\,dx$ must be positive. The other function may give negative integral on some limits.

 

[Gary Smart]

Why must the parabola be positive? is that because we are subtracting the other function away from it, thus a negative subtracting a negative will always be a negative. Therefore will never give an area of 1?

Does the parabola have to be the first function? or can the line be function 1?

 

[theodoros.mihos]

Make a simple google graph to see the shapes.

 

[Gary Smart]

Both of these sets of functions are allowed in the constraints of this question.

 

[theodoros.mihos]

Function 1: 6x^2 - 2x + 8
Function 2: 4x + 8
This problem represented by the second graph.

 

[Gary Smart]

Function 1: 6x^2 - 2x + 8
Function 2: 4x + 8
This problem represented by the second graph.

These functions give an area of 1 but the only reason I know why is when function 2's area is subtracted by function's 1 it gives an area of 1 (Parabolic segment). I don't know why else it works.

 

[theodoros.mihos]

This is correct. See the axis units.

 

[Gary Smart]

This is correct. See the axis units.

I know the x-axis units of intersection are 0 and 1. But using these units doesn't always work.

 

[theodoros.mihos]

You make a coefficient error on your post, but I think this is typo, because you make the correct calculation

Curve: 3x^2 - x^2 + 8x [Boundaries of 0 and 1]: Area under curve = 9 (between 0 and 1). ---> 2x^3 ...

Line: 2x^2 + 8x [Boundaries of 0 and 1]; Area under line = 10 (Between 0 and 1).

 

[Gary Smart]

Okay, I get that. Is there a way of investigating this algebraically? Maybe proofing it e.g. if I wanted to find more areas of 1 in the first quadrant using a parabola and a line?

 

[theodoros.mihos]

See this

 

[Gary Smart]

The trapezoidal rule will only give me the area the area under the line though?

 

[theodoros.mihos]

By the same way for all functions.

 

[Gary Smart]

So, I need to apply the trapezoidal rule in general to general forms of both types of functions?

 

[theodoros.mihos]

No, trapezoidal rule is the discrete case (used on computational calculations) for the same think we make with calculus by integrals. Integrals are limits with $\Delta{x}\to0$ for the trapezoidal rule.

 

[Gary Smart]

Ahhh. I see. So there isn't a way of finding an area of 1 with these restrictions using algebra?

 

[Gary Smart]

I've carried out some investigations involving altering values of the quadratic then change the gradient of the line to get an area of 1.

I think all the combinations of the quadratic can fit into the investigations carried out in that table. I haven't really seen any patterns though...

 

[momoko]

Simpson's rule can be used to calculate integrals of polynomial up to degree 3 exactly. It may make your life easier.

 

[LCKurtz]

I see lots of replies since I was here last. But, @Gary Smart, I see where you want to do it algebraically but you haven't followed my original suggestion to get started. I suggested you consider a special, easier, case to get started. Consider the upward opening parabola $y = (x-a)^2$ and the line $y=mx$ with $a\ge 0,~m\ge 0$. This parabola's vertex is at $(a,0)$ and the line passes through the origin into the first quadrant. If the intersection points $x$ values are $u$ and $v$, the area between the line and the parabola is$$
A = \int_u^v mx - (x-a)^2~dx$$You want some algebra? Here's some algebra for you. Solve for the $x$ values of $u$ and $v$ where the line intersects the parabola. Then put those in for the limits in the integral above and set the integral equal to $1$. Work it through and it will give you an equation for $m$ in terms of $a$. So each such parabola has a corresponding line and slope. That could be a start for your analysis.

 

[Gary Smart]

I see lots of replies since I was here last. But, @Gary Smart, I see where you want to do it algebraically but you haven't followed my original suggestion to get started. I suggested you consider a special, easier, case to get started. Consider the upward opening parabola $y = (x-a)^2$ and the line $y=mx$ with $a\ge 0,~m\ge 0$. This parabola's vertex is at $(a,0)$ and the line passes through the origin into the first quadrant. If the intersection points $x$ values are $u$ and $v$, the area between the line and the parabola is$$
A = \int_u^v mx - (x-a)^2~dx$$You want some algebra? Here's some algebra for you. Solve for the $x$ values of $u$ and $v$ where the line intersects the parabola. Then put those in for the limits in the integral above and set the integral equal to $1$. Work it through and it will give you an equation for $m$ in terms of $a$. So each such parabola has a corresponding line and slope. That could be a start for your analysis.

Just to make sure I'm clear. That equation involves integrating the general form of a line and parabola simultaneously. The u and v values are the points of interception as we are trying to find the area between these bounds.

How do I solve for x though with no values?