Geometrical books (differential geometry, tensors, variational mech.)

[Idun]

I am looking for math books that focus on geometrical interpretations. Sadly most of the modern books lack these interpretations and only consists out of theorems and proofs. It seems to me that most modern mathematicians are pure left-brain sequential thinkers that do not have a lot of visualization capabilities.

I did some prior research on differential geometry, tensor calculus and variational mechanics and luckily Dover publishes really cheap but good books on these topics. My most recent purchases are:

-> Lectures on Classical Differential Geometry (Dirk Struik)
-> Lagrangian and Hamiltonian Mechanics (Calkin)
-> The variational principles of Mechanics (Cornelius Lanczos)
-> Vector and Tensor Analysis with Applications (Borisenko & Tarapov)

Some former threads mention Do Carmo but a quick glance in the ebook tells me it doesn't offer anything new.

Other books who are on my radar are "Geometry of Physics" by Theodore Frankel (hence why post is in this topic) and "Geometry, Topology and Physics" by Nakahara. Sadly I can't find pdf's of these to look into. (I always buy the books that I like, I just take precautions)

EDIT: I found Nakahara but for a geometry book, it doesn't contain a lot of geometrical pictures. I am looking for geometrical insights like for example Pythagoras visual proof:

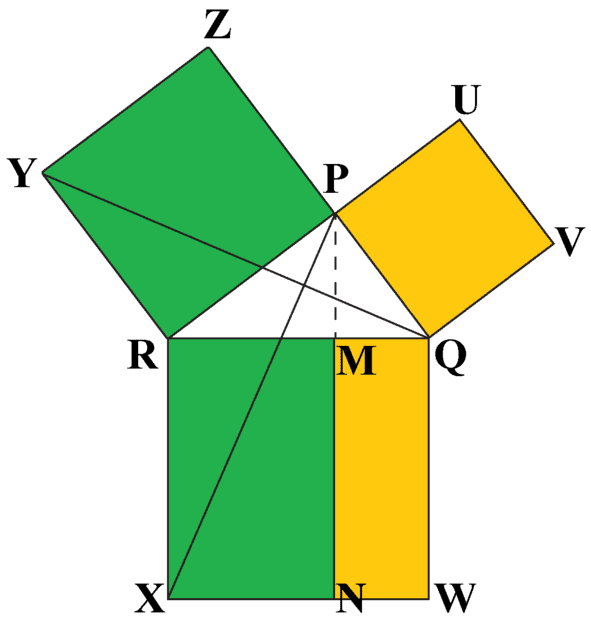https://mathoverflow.net/questions/...ch-technical-detail-and-so-little-enlightenme

 

[mathwonk]

try david hilbert: geometry and the imagination, and david henderson: differential geometry, a geometric introduction.

 

[Daverz]

I do recommend the Frankel book because of the careful pedagogy that's gone into it. As far as I can tell, there's not much compelling in the 2nd edition if you can find a cheaper copy of the 1st edition.

Tristan Needham's new "visual" book on differential geometry should be available soon. You can preview it on Amazon:

https://www.amazon.com/dp/0691203709/?tag=pfamazon01-20

Similar books in this vein are

Jon Pierre Fortney, A Visual Introduction to Differential Forms and Calculus on Manifolds
David Bachman, A Geometric Approach to Differential Forms 2nd ed.

The Bachman book is an easy read.

I'd also recommend studying the "classical" theory of curves and surfaces. I like the book by Millman & Parker, Elements of Differential Geometry.