MHB [Geometry + Algebra] Integrated Questions

[rtwikia]

View attachment 4969

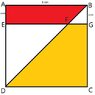
In the figure, ABCD is a square of side 1 cm. ABFE and CDFG are trapeziums(/trapeziods?). The Area of CDFG is twice the Area of ABFE. Let x cm be the length of AE.

(a) Express the length of FG in terms of x.

(b) Find the value of x, correct to 2 decimal places.

Thanks! :D

 

[MarkFL]

Hello and welcome to MHB, rtwikia! :D

We ask that our users post what they have tried so that we best know how to help, as we can then see where you are stuck or may be going wrong.

To answer part a), we could use the formula for the area of a trapezium/trapezoid and the information given about the areas of the two shaded areas. Using this formula:

$$A=\frac{h}{2}(B+b)$$

We may then write:

$$\frac{\overline{CG}}{2}(\overline{CD}+\overline{FG})=2\cdot\frac{\overline{AE}}{2}(\overline{AB}+\overline{EF})$$

Now, we know the following (all measures are in cm):

$$\overline{CG}=1-x$$

$$\overline{CD}=1$$

$$\overline{AE}=x$$

$$\overline{AB}=1$$

$$\overline{EF}=1-\overline{FG}$$

Can you now use all of this to write an equation involving only $$\overline{FG}$$ and $x$, for which you can then solve for $$\overline{FG}$$?

 

[rtwikia]

I got

$\frac{1-x}{2}\left(1+\overline{FG}\right)=x\left(2-\overline{FG}\right)$

Am I right? :D

 

[MarkFL]

I got

$\frac{1-x}{2}\left(1+\overline{FG}\right)=x\left(2-\overline{FG}\right)$

Am I right? :D

First, I just wanted to let you know I wrapped the $\LaTeX$ code you posted with $$$$ tags so it would be parsed as such.

Yes, your equation is correct. Now, you are asked to express $\overline{FG}$ in terms of $x$, so you need to solve that equation for $\overline{FG}$. :)

 

[rtwikia]

...
Yes, your equation is correct. Now, you are asked to express $\overline{FG}$ in terms of $x$, so you need to solve that equation for $\overline{FG}$. :)

After simplification, I found that $\overline{FG}=\frac{5x-1}{1+x}$. Can it be simplified further or is this the final answer? (When I measure the picture it measures nearly excatly $x$ cm)

 

[MarkFL]

After simplification, I found that $\overline{FG}=\frac{5x-1}{1+x}$. Can it be simplified further or is this the final answer? (When I measure the picture it measures nearly excatly $x$ cm)

Excellent! I also obtained:

$$\overline{FG}=\frac{5x-1}{x+1}$$

Now, about your measurement...which will lead us to be able to answer part (b) of the exercise, we should be able to see that $$\triangle BFG$$ and $$\triangle BDC$$ are similar. This similarity allows us to write:

$$\frac{x}{\overline{FG}}=\frac{\overline{BC}}{\overline{DC}}$$

Now, since $\overline{BC}=\overline{DC}=1$, this leads us to conclude:

$$\overline{FG}=x$$

And then taking our previous result, we may then equate our two expressions, and write:

$$x=\frac{5x-1}{x+1}$$

This will lead to a quadratic, where we should discard any roots unless we find $0<x<1$. What do you find?

 

[rtwikia]

...

Now, about your measurement...which will lead us to be able to answer part (b) of the exercise, we should be able to see that $$\triangle BFG$$ and $$\triangle BDC$$ are similar. This similarity allows us to write:

$$\frac{x}{\overline{FG}}=\frac{\overline{BC}}{\overline{DC}}$$

Now, since $\overline{BC}=\overline{DC}=1$, this leads us to conclude:

$$\overline{FG}=x$$

...

I've noted that it isn't given that $BFD$ is a straight line. Does it affect the deduction process?

 

[MarkFL]

I've noted that it isn't given that $BFD$ is a straight line. Does it affect the deduction process?

Without assuming $\overline{BD}$ is a diagonal of the square $ABCD$, I don't see how we can find the value of $x$. :)

 

[rtwikia]

Without assuming $\overline{BD}$ is a diagonal of the square $ABCD$, I don't see how we can find the value of $x$. :)

Okay then. And thanks by the way. I got the answer $0.27$ already.(Rock)

 

[MarkFL]

Okay then. And thanks by the way. I got the answer $0.27$ already.(Rock)

Yes, I found $x=2-\sqrt{3}\approx0.27$ as well. :D