Given an acceleration figure calculate speed and distance

[Alexanddros81]

Homework Statement

Serway Physics Chapter 2
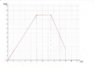
19. A particle starts from rest and accelerates as shown in Figure P2.19.
Determine (a) the particle's speed at t = 10.0s and at t = 20.0s and
(b) the distance traveled in the first 20.0s

Homework Equations

The Attempt at a Solution

I am confused with the slope from t = 15s to t = 20s.
Calculating from given fiure: $slope = \frac {v} {5s} => v = (-3)(5) = -15m/s$
I suppose I add the -15m/s to 20m/s to give 5m/s which is the velocity at t=20s
Is this the correct way to calculate the speed at 20s?
or I just calculate the areas of the a-t figure?

(b) for this part I calculated the area of the trangle then the area of the rectangle and the are of the
trapezoid under the v-t graph and added them all together

 

[kuruman]

Everything looks fine.

Is this the correct way to calculate the speed at 20s?
or I just calculate the areas of the a-t figure?

Either way is correct. Just remember that in this case the first area is positive and the second is negative.