Given circle, find the line of bearing of tan lines thru 0,0

[srcs]

This question occurred to me a few days ago and it's been bugging me ever since.

Consider a circle in the coordinate plane with center P(x,y) and radius R, where R < D, D being the distance from the origin to the circle's center.

There are two lines tangent to the circle (T₁ and T₂) that pass through the origin.

The circle's location can also be considered as a line segment of radius D and some angle Θ with the x axis.

How can I find a general equation in terms of x, y, R, and Θ to determine the angle each tangent line makes with the x axis?

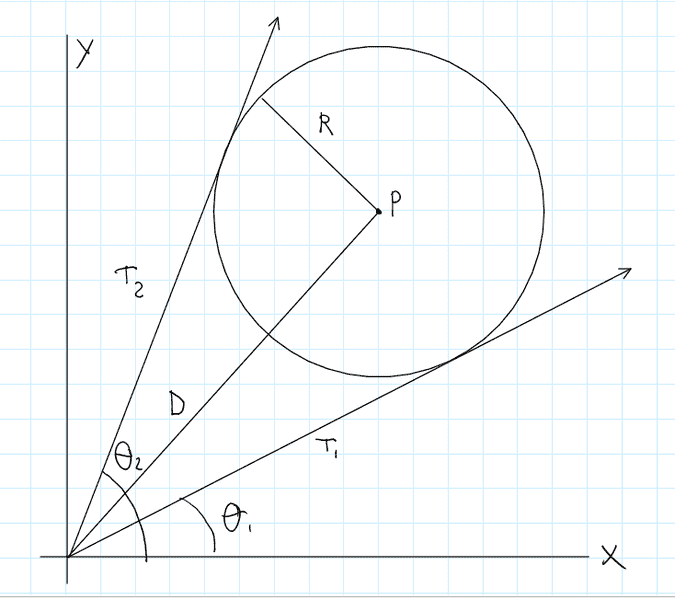
Solution found:

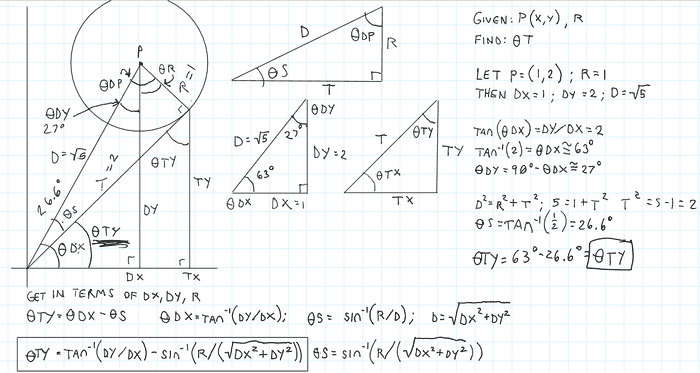
Adding Θ_s to Θ_dx should yield the bearing for the other tangent line.

 

[jedishrfu]

You might consider that where the line hits the circle it will be perpendicular to some radius so you have some D length and some angle that D makes with the X axis and some trig to mix into get your answer.

 

[srcs]

You might consider that where the line hits the circle it will be perpendicular to some radius so you have some D length and some angle that D makes with the X axis and some trig to mix into get your answer.

Solved. The help is appreciated.

 

[srcs]

I can't tell if this is just a coincidence of the values I chose, but the distance from the x-axis to the circle's center (Dy) worked out to be equal to the distance from the origin to the tangent line's intersection (T). Weird.

 

[jedishrfu]

I can't tell if this is just a coincidence of the values I chose, but the distance from the x-axis to the circle's center (Dy) worked out to be equal to the distance from the origin to the tangent line's intersection (T). Weird.

This may be a theorem and might be proven if you think about it more abstractly. You are actually saying that drawing a circle with center at the origin that passes through the original circle's center will intersect at the tangent line points.

Perhaps @Mark44 could verify your observation and point to the theorem if it exists as I don't know for sure.

Edit: okay I think this is it on Wikipedia

https://en.m.wikipedia.org/wiki/Tangent_lines_to_circles

Look down a bit in the article to see two intersecting circles and how tangent lines from one circle go through the center of another.

 

[srcs]

This may be a theorem and might be proven if you think about it more abstractly. You are actually saying that drawing a circle with center at the origin that passes through the original circle's center will intersect at the tangent line points.

Perhaps @Mark44 could verify your observation and point to the theorem if it exists as I don't know for sure.

Edit: okay I think this is it on Wikipedia

https://en.m.wikipedia.org/wiki/Tangent_lines_to_circles

Look down a bit in the article to see two intersecting circles and how tangent lines from one circle go through the center of another.

Thanks, this is interesting. Also I just noticed an error in my second diagram when I renamed my variables: Θ_ty should beΘ_tx everywhere except in the cutout triangle, where it's correctly labeled. I'm pretty sure the calculations themselves are still correct. I'll update the image.

Never mind, the OP no longer has an edit option. I'll just post it here.