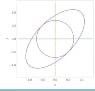
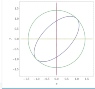
The discussion centers on finding the points on a curve that are nearest to the origin, specifically addressing a problem involving a tilted ellipse described by the equation 5x² - 6xy + 5y² = 4. Participants explore methods to minimize the distance from the origin, emphasizing the use of calculus and the first derivative to find maxima and minima. They clarify that the curve is not a circle but an ellipse, and suggest using polar coordinates or transformations to simplify the problem. Ultimately, they identify that the closest points to the origin are (1,1) and (-1,-1), confirming their validity by checking against the original equation. The conversation highlights the importance of visualizing the problem and considering different approaches to arrive at a solution efficiently.