- #1
Karol
- 1,380
- 22
Homework Statement
Homework Equations
First derivative=maxima/minima/vertical tangent/rising/falling
When f'(x)>0 ? the function rises
The Attempt at a Solution
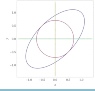
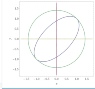
Deriving relative to x:
$$10x-6(yy'+x)+10yy'=0~\rightarrow~y'=-\frac{x}{y}$$
What do i do with that?
Attachments
Last edited by a moderator: