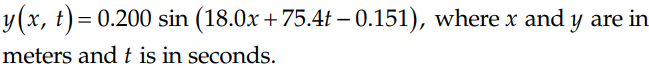SUMMARY
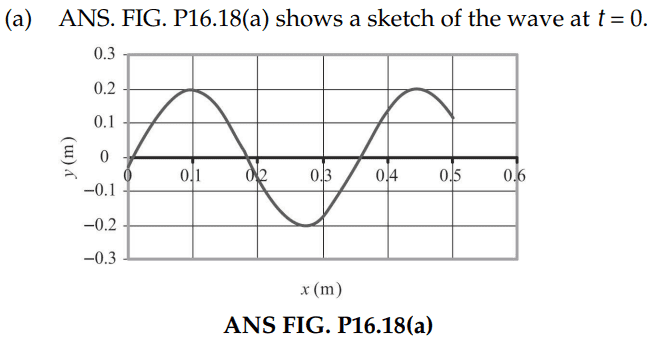
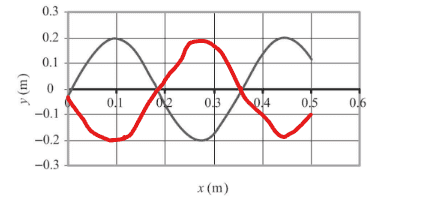
The discussion centers on understanding the behavior of a sinusoidal wave traveling in the negative x-direction and its implications for an object, such as a basketball, dropped at the wave's peak. Participants clarify that while an ideal transverse wave would keep the basketball stationary in vertical motion, realistic surface waves involve both transverse and longitudinal components, causing the basketball to drift leftward. The key takeaway is that at t=0, the element at x=0 has a positive upward velocity, and the waveform's movement must be accurately represented to reflect this behavior over time.
PREREQUISITES
- Understanding of sinusoidal wave properties
- Familiarity with transverse and longitudinal wave concepts
- Basic knowledge of simple harmonic motion
- Ability to interpret graphical representations of waveforms
NEXT STEPS
- Study the mathematical representation of sinusoidal waves
- Learn about the principles of wave propagation in different media
- Explore the effects of wave interference on object motion
- Investigate the relationship between wave velocity and particle velocity in oscillatory systems
USEFUL FOR
Students and educators in physics, particularly those focusing on wave mechanics, as well as anyone interested in the practical implications of wave behavior in real-world scenarios.