You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Gravitational Plot: Accuracy Checked
- Thread starter Invutil
- Start date
-
- Tags
- Gravitational Plot
AI Thread Summary
The discussion centers on the validity of various equations related to gravity and motion. The first equation assumes constant acceleration, while the second involves variable acceleration, making them incompatible for direct use together. The complexity of planetary motion requires a different approach, as it involves universal gravitation and non-constant acceleration. Numerical integration is suggested for accurately modeling motion under varying forces, rather than relying on simplified formulas. The conversation highlights the need for a deeper understanding of the mathematics involved in gravitational dynamics, especially when considering scenarios like negative radius values.
Physics news on Phys.org
Chandra Prayaga
Science Advisor
- 652
- 150
No. The first equation assumes that the acceleration is a constant. The second equation does not give a constant acceleration, so you cannot use the acceleration from the second in the first equation I don't know where you got equ 3 from. Perhaps if you stated the problem?
- 29,138
- 20,767
Can you explain what you're trying to do? I don't understand the third equation, nor the graphs.
Invutil
- 24
- 0
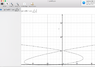
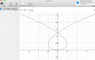
I'm just plotting gravity free-fall.
r = (x2 - x) for x2 > x where x2 is the coordinate of mass 2
Is this correct?
x(t) = x0 + int from {0} to {t} ( v0 t + 1/2 a0 t^2 + int from {0} to {t} ( 1/2 t^2 da/dt ) dt ) dt
a0 = F/m1
a0 = G m2 / r0^2
r0 = (x2 - x0)
x(t) = x0 + int from {0} to {t} ( v0 t + 1/2 G m2 t^2 / (x2-x0)^2 + int from {0} to {t} ( d( 1/2 t^2 G m2 / (x2 - x(t))^2 )/dt ) dt ) dt
I can't get this to plot, but should there be anything special at negative radius values?
r = (x2 - x) for x2 > x where x2 is the coordinate of mass 2
Is this correct?
x(t) = x0 + int from {0} to {t} ( v0 t + 1/2 a0 t^2 + int from {0} to {t} ( 1/2 t^2 da/dt ) dt ) dt
a0 = F/m1
a0 = G m2 / r0^2
r0 = (x2 - x0)
x(t) = x0 + int from {0} to {t} ( v0 t + 1/2 G m2 t^2 / (x2-x0)^2 + int from {0} to {t} ( d( 1/2 t^2 G m2 / (x2 - x(t))^2 )/dt ) dt ) dt
I can't get this to plot, but should there be anything special at negative radius values?
Attachments
- 29,138
- 20,767
You seem to be mixing up two different gravitational equations: one for a constant force (valid, for example, near the surface of the Earth); and one for a variable force (valid, for example, for planetary motion).
The first of these is mathematically simple; the second is mathematically much more complicated.
The first of these is mathematically simple; the second is mathematically much more complicated.
Invutil
- 24
- 0
I guess I'm dealing with planetary scales so radius comes into effect. Is there a formula I can use? Is there anything special that happens at negative radius, like, a Kerr black hole, using a Newtonian equation? Would the constant-acceleration formula generally be correct, as it is a Taylor expansion? If so, how do you interpret the trajectory after r < 0?
- 29,138
- 20,767
Invutil said:I guess I'm dealing with planetary scales so radius comes into effect. Is there a formula I can use? Is there anything special that happens at negative radius, like, a Kerr black hole, using a Newtonian equation? Would the constant-acceleration formula generally be correct, as it is a Taylor expansion? If so, how do you interpret the trajectory after r < 0?
It depends how much maths you know. The planetary motion equation leads to a second-order differential equation, from which Kepler's laws can be deduced. For free fall, say of an asteroid towards the Earth, the equation can be solved with some difficulty.
Chandra Prayaga
Science Advisor
- 652
- 150
I think you are trying to over-simplify the problem. Your equations are still valid only for constant acceleration. Planetary motion, including that of asteroids, is described using universal gravitation for the force, and the acceleration is not constant. If you want to use the constant acceleration formula, than you have to numerically integrate the equations of motion, using short intervals of time, during which you assume that the acceleration is constant. That becomes a job to be done by a computer, and not a simple formula into which you can substitute numbers.
Similar threads
- Replies
- 9
- Views
- 2K
- Replies
- 6
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 11
- Views
- 2K
- Replies
- 15
- Views
- 745
- Replies
- 1
- Views
- 2K
- Replies
- 14
- Views
- 2K
- Replies
- 4
- Views
- 1K
- Replies
- 7
- Views
- 1K
- Replies
- 19
- Views
- 3K
Hot Threads
-
I Explain Bernoulli at the molecular level?
- Started by user079622
- Replies: 251
- Classical Physics
-
B Simple mass/scale puzzle
- Started by DaveC426913
- Replies: 206
- Classical Physics
-
I Solving a momentum problem where masses change after the collision
- Started by rdemyan
- Replies: 35
- Classical Physics
-
B Formal definition of work done
- Started by physicals
- Replies: 48
- Classical Physics
-
I Topic about physics axioms, theory, laws etc..
- Started by user079622
- Replies: 93
- Classical Physics
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math