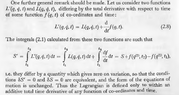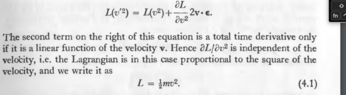- #1
gionole
- 281
- 24
- TL;DR Summary
- Lagrangian when adding total time derivative
When we have ##L(q, \dot q, t)##, The change in action is given by:
##\int_{t_1}^{t_2} dt (\frac{\partial L}{\partial x} f(t) + \frac{\partial L}{\partial \dot x} \dot f(t))## when we change our true path ##x(t)## by ##x(t) + \epsilon f(t)##.
Now, attaching the image, check what Landau says.
I'm wondering whether he means that in the ##f(q,t)##, whether q also depends on ##t## or not.
Let's say It doesn't. In this case, when we change ##x(t)## by ##x(t) + \epsilon f(t)##, change in lagrangian ##dL = \frac{\partial L}{\partial x} dx + \frac{\partial L}{\partial \dot x} d\dot x## . What I did in there is even when true path changed with variation, ##f(q,t)## stayed the same in the new lagrangian(it didn't change), and we directly got dL to be the same as if we had used variation for only ##L(q, \dot q, t)## and not ##L(q, \dot q, t) + \frac{d}{dt}f(q,t)##. In this case, if lagrangian didn't change, action wouldn't change and the derivation of euler lagrange would be for the same action as for the ##L(q, \dot q, t)##. Would this logic apply ? but i also realize that this is only valid if ##f(q,t)## is just an ordinary function of some coordinate and time where coordinate doesn't act like in the same way as it does in the L itself. The coordinate in L is a function of t in itself.
Another way would be to just treat ##L'(q, \dot q, t)## as the normal lagrangian(just imagine that it doesn't include ##\frac{d}{dt}f(q,t)## and once I get to ##\int_{t1}^{t2} (\frac{\partial L}{\partial x} - \frac{d}{dt}\frac{\partial L}{\partial \dot x}) dt f(t)##, I could just plug in instead of L, the ##L +\frac{d}{dt}f(q,t)## and this still proves the equation of motion will be the same, but this here only would be correct if ##f(q,t)## is 0 at ##t2## and ##t1##.
Please note that ##\frac{d}{dt}f(q,t)## is not the same thing as ##\epsilon f(t)## we use for variation of true path(at least this is my undestanding). So would my first way be correct ? is ##f(q,t)## such a function where q is just coordinate and nothing more(not a function of ##t##) ? or my 2nd way is correct which assumes that this ##f(q,t)## has to be 0 at t2 and t1 ?
##\int_{t_1}^{t_2} dt (\frac{\partial L}{\partial x} f(t) + \frac{\partial L}{\partial \dot x} \dot f(t))## when we change our true path ##x(t)## by ##x(t) + \epsilon f(t)##.
Now, attaching the image, check what Landau says.
I'm wondering whether he means that in the ##f(q,t)##, whether q also depends on ##t## or not.
Let's say It doesn't. In this case, when we change ##x(t)## by ##x(t) + \epsilon f(t)##, change in lagrangian ##dL = \frac{\partial L}{\partial x} dx + \frac{\partial L}{\partial \dot x} d\dot x## . What I did in there is even when true path changed with variation, ##f(q,t)## stayed the same in the new lagrangian(it didn't change), and we directly got dL to be the same as if we had used variation for only ##L(q, \dot q, t)## and not ##L(q, \dot q, t) + \frac{d}{dt}f(q,t)##. In this case, if lagrangian didn't change, action wouldn't change and the derivation of euler lagrange would be for the same action as for the ##L(q, \dot q, t)##. Would this logic apply ? but i also realize that this is only valid if ##f(q,t)## is just an ordinary function of some coordinate and time where coordinate doesn't act like in the same way as it does in the L itself. The coordinate in L is a function of t in itself.
Another way would be to just treat ##L'(q, \dot q, t)## as the normal lagrangian(just imagine that it doesn't include ##\frac{d}{dt}f(q,t)## and once I get to ##\int_{t1}^{t2} (\frac{\partial L}{\partial x} - \frac{d}{dt}\frac{\partial L}{\partial \dot x}) dt f(t)##, I could just plug in instead of L, the ##L +\frac{d}{dt}f(q,t)## and this still proves the equation of motion will be the same, but this here only would be correct if ##f(q,t)## is 0 at ##t2## and ##t1##.
Please note that ##\frac{d}{dt}f(q,t)## is not the same thing as ##\epsilon f(t)## we use for variation of true path(at least this is my undestanding). So would my first way be correct ? is ##f(q,t)## such a function where q is just coordinate and nothing more(not a function of ##t##) ? or my 2nd way is correct which assumes that this ##f(q,t)## has to be 0 at t2 and t1 ?