Newtons Apple
- 73
- 1
Ok... if there's one thing that really rustles my jimmies...is when I look at an equation an it's chock filled of greek letters, in a big swirl of greek alphabet soup...
I have a question, when you approach a new equation, do you automatically know what the symbols mean? Is it relative to the type of equation? I was looking at this, in regards to
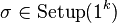
and
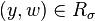
Are the two greek letters here, epsilon and sigma(?), always to refer to the same thing for every problem? How do you know then what they refer to? I see a lot of problems where they don't specify what the symbols mean? I look online and I get varying answers.
Is there a set way that one should "read" a statement like the one below? And more specifically what on Earth does epsilon stand for here, and how do you know?
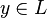
I have a question, when you approach a new equation, do you automatically know what the symbols mean? Is it relative to the type of equation? I was looking at this, in regards to
and
Are the two greek letters here, epsilon and sigma(?), always to refer to the same thing for every problem? How do you know then what they refer to? I see a lot of problems where they don't specify what the symbols mean? I look online and I get varying answers.
Is there a set way that one should "read" a statement like the one below? And more specifically what on Earth does epsilon stand for here, and how do you know?