Heat distribution in a piece of glass receiving protons

[Bqback]

Homework Statement

A glass piece with dimensions LxLxH mm is sitting on a cooled table (with constant temp T0) and receiving a stream of protons with given stream density φ (protons/(cm^2*s)) and energy per proton Ep from above.
Density ρ , specific heat capacity c_p, heat conductivity κ, emissivity ε are all given.
Using the finite difference method, find heat distribution for varying stream densities and estimate heat eradiated from the glass piece's surface.

Relevant Equations

dT/dt = a^2 * d^2T/dx^2 + f(x) is the standard heat equation.
f(x), the source function is replaced by an array of data points that show the distribution of absorbed energy (in keV/(proton*μm)) throughout the H dimension within a very narrow band (from 0.006 μm to 0.51 μm).

First of all, I didn't know whether to pick this subforum or the engineering/compsci one, I understand this might need to be moved to a more appropriate subforum.
The general approach is fairly obvious, use implicit method to construct the tridiagonal matrix for Thomas method and solve. However, I'm having problems bringing heat transfer on the "outer side" facing the stream into the mix. I assumed the initial condition is the same temperature all throughout the piece, and the face touching the table will obviously have the same temperature regardless of time.

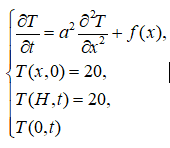
My first (and only) idea so far was comparing energy received from protons and radiated away:

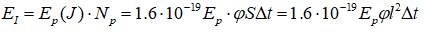
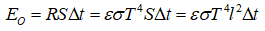
For heat capacity C I used a small slice along H (from 0 to the first point in distribution data)

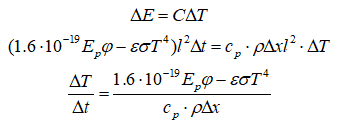
However, implementing this as a finite difference

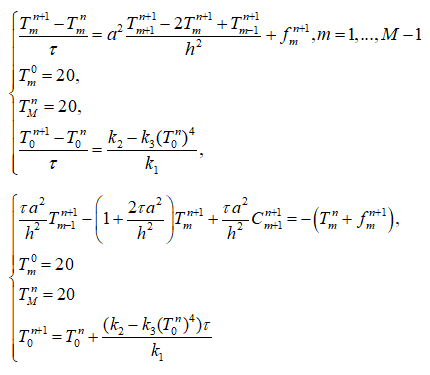
always leads to not only huge endless divergencies (on the orders of magnitude far beyond humanly achievable), but even negative temperatures for sufficiently small (10^`11 or less) φ. I've spent a lot of time tinkering with coefficients and trying different things with my code but it never worked out. Closest I got to something resembling normal behavior is T^n_0 aproaching a value, but the value and the "approach speed" is the same regardless of φ, which doesn't make much sense physically.

My second idea so far has been to flat out assign a value to temperature on the outer face (e. g. the temperature at the nearest point), but then I still have no idea how to bring in heat radiation.

 

[Chestermiller]

You are saying you don't now how to include the boundary condition at x = 0 into your finite difference scheme?

 

[Bqback]

You are saying you don't now how to include the boundary condition at x = 0 into your finite difference scheme?

Sorry, I meant I don't know what the boundary condition should be, I know how to include it. The approach I described is the only one I could come up with but it doesn't seem to work.

 

[Chestermiller]

Sorry, I meant I don't know what the boundary condition should be, I know how to include it. The approach I described is the only one I could come up with but it doesn't seem to work.

You don't include the energy from the photon flux in the BC. That energy is released within the glass. Also, there is thermal radiation from the surroundings that needs to be included. Is that what you are calling k2? And the BC doesn't include a thermal inertia term. It is only heat conduction flux $-k\frac{\partial T}{\partial x}$ within the glass at the boundary is equal to the radiative heat flux from the surroundings minus the radiative heat

 

[Chestermiller]

In particular,the BC at x = 0 should read:
$$-k\frac{\partial T}{\partial x}=\epsilon \sigma(T_{\infty}^4- T^4)+h(T_{\infty}-T)$$where h is the convective heat transfer coefficient and $T_{\infty}$ is the bulk room temperature away from the surface.

 

[Bqback]

You don't include the energy from the photon flux in the BC. That energy is released within the glass. Also, there is thermal radiation from the surroundings that needs to be included. Is that what you are calling k2? And the BC doesn't include a thermal inertia term. It is only heat conduction flux $-k\frac{\partial T}{\partial x}$ within the glass at the boundary is equal to the radiative heat flux from the surroundings minus the radiative heat

Isn't $E_I$the energy from the photon flux? Also, I forgot to mention all of this is happening in a vacuum, if that changes anything.

 

[Chestermiller]

I assume that the imposed photon flux only occurs in a very limited range of wavelengths, and it results in heating within the glass only by absorption of photons by the glass (described by the generation term in your equation). Is this the case? If so, and the process takes place in vacuum, then the BC becomes: $$-k\frac{\partial T}{\partial x}=\epsilon \sigma(T_{\infty}^4- T^4)$$ where T infinity is the temperature within the room (such that the glass also receives a broad spectrum of radiation from the room). This reflects the condition that, if the glass is at the same temperature as the room and the imposed photon flux is zero, the glass temperature won't change.