SUMMARY
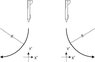
The discussion centers on calculating the height at which a pilot must pull out of a vertical dive to avoid exceeding a maximum acceleration of 5g. The jet's speed is constant at 1200 km/h, and the calculations involve understanding centripetal acceleration. Participants clarify that the effective acceleration experienced by the pilot includes both gravitational force and the centripetal force required for the turn. The final conclusion indicates that the radius of the turn must be at least 2263 meters to ensure the pilot does not lose consciousness during the maneuver.
PREREQUISITES
- Understanding of centripetal acceleration and forces in circular motion
- Familiarity with gravitational acceleration (9.8 m/s²)
- Knowledge of basic physics equations, particularly F = ma
- Ability to perform calculations involving units of acceleration (g's)
NEXT STEPS
- Study the principles of circular motion and centripetal force in detail
- Learn how to apply the equations of motion for objects in free fall
- Explore the effects of g-forces on human physiology during flight maneuvers
- Investigate the dynamics of jet aircraft during high-speed turns and dives
USEFUL FOR
Aerospace engineers, pilots, physics students, and anyone interested in the dynamics of flight and the effects of acceleration on human bodies in aviation contexts.