- #1
mastergaurang
- 1
- 0
Homework Statement
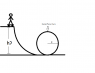
The attachment shows the problem. The normal force at the top of the loop is 3 g's (as in g-force).
Homework Equations
PE = mgh
KE = .5mv2
Fc = [itex]\frac{mv2}{r}[/itex]
PE + KE = PE' + KE'
v = [itex]\sqrt{2gh}[/itex]
The Attempt at a Solution
The normal force would be: 30 * mass.
Since he's at the top of the loop, the formula would be:
Fnet = Fc = (mv2)/r = Fnormal + mg
I have tried to cancel the mass out and to formulate a system of equations but I think I'm missing something. One formula I got is by setting PE equal to KE (for h, but only at the bottom before the skater goes up the loop):
h = [itex]\frac{.5v2}{g}[/itex]
I am starting to think that I need the radius/velocity. Any ideas?