Help with a Bending Stress Calculation

[Joe591]

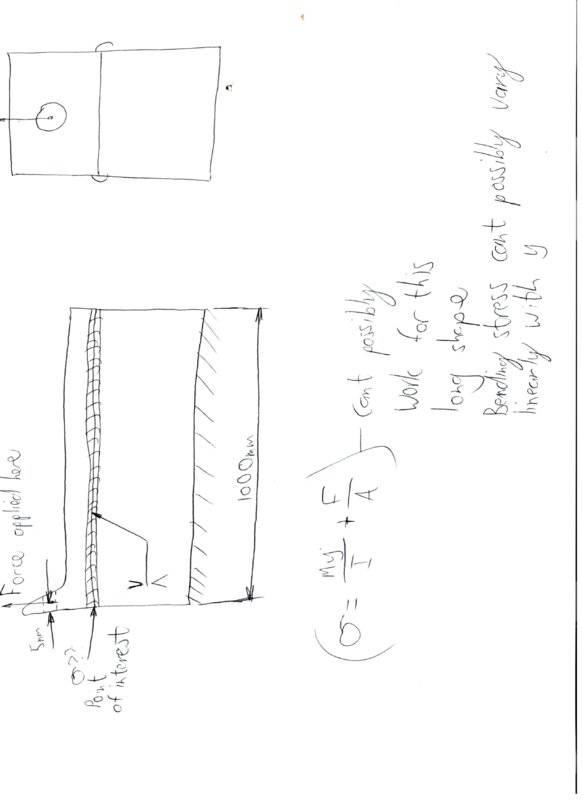
I've attached a photo of a "problem". How would you calculate the stress at the area in question? I seriously doubt that the bending stress would vary linearly throughout the whole meter of total length of the section. I would expect it to become zero long before it reaches the opposite extremity. Please point me in the direction of an applicable text. An online source would be nice... Really hope the picture is clear...

 

[haruspex]

I am unable to interpret your diagram. Please add some labels and provide a verbal description that refers to them.

 

[Joe591]

Okay, I'll simplify it because for the sake of the question you don't actually need all that detail. Here is a hypothetical block. You'll notice that the one side is much longer than the rest. If you apply normal, run of the mill bending theory to this it would be by means of this equation:

Stress = F/A + My/I

What I would like to know is if that equation still holds for a case where one side is much longer than the rest. If it doesn't, what is a good source for the necessary research.

 

[haruspex]

Okay, I'll simplify it because for the sake of the question you don't actually need all that detail. Here is a hypothetical block. You'll notice that the one side is much longer than the rest. If you apply normal, run of the mill bending theory to this it would be by means of this equation:

Stress = F/A + My/I

What I would like to know is if that equation still holds for a case where one side is much longer than the rest. If it doesn't, what is a good source for the necessary research.
View attachment 246099

That's much clearer, but somewhat unexpected. Please confirm that the rigid attachment runs the whole length of the beam, on the far side from the applied pull. (I.e. all the way down the vertical rear of the beam as shown by the dashes in the diagram.)
If so, that certainly makes it different from any scenario I've seen before. Maybe my ignorance, but neither do I recognise the equation you quoted. What is A there? Do you have link to a source of the equation?

 

[Joe591]

It's basically this (see picture), except the one side is exaggerated and the force is in the opposite direction. Yes the side that is constrained is fully constrained over it's entire surface. It's basically an extreme case of eccentric loading.

F is force
A is area
M is moment
y is distance from the neutral axis at which the stress is being calculated.
I is second moment of area. The picture came from https://theconstructor.org/tips/types-columns-building-construction/24764/

 

[haruspex]

It's basically this (see picture), except the one side is exaggerated and the force is in the opposite direction. Yes the side that is constrained is fully constrained over it's entire surface. It's basically an extreme case of eccentric loading.

View attachment 246101F is force
A is area
M is moment
y is distance from the neutral axis at which the stress is being calculated.
I is second moment of area.The picture came from https://theconstructor.org/tips/types-columns-building-construction/24764/

Ok, so with reference to your diagram in post #3, e_y is the distance down from the midpoint of the block to where P (or F) is applied, right?
I see no reason why the formula you quote would not apply, but note that it means the top part could be under tension while the bottom is under compression. This may cause your intuition to mislead you.

I found this link helpful https://www.ecourses.ou.edu/cgi-bin/ebook.cgi?doc=&topic=me&chap_sec=09.3&page=theory

 

[jrmichler]

Looking at your post #3, the beam bending plus F/A equation does not apply.

My/I is for the bending stresses in a "long" beam. A long beam has the length several times longer than the depth (height) of the beam. That equation only applies at points far from stress concentrations. Search St. Venant's Principle for more information. Here is a good link to get started: https://coefs.uncc.edu/mwhelan3/files/2010/10/ICD_Saint_Venant1.pdf.

As a general rule of thumb, if H is the depth (height) of the beam, then My/I does not apply for a distance of 1D from each point of load application or support point.

Similar constraints apply to F/A.

There are analytic solutions for some special cases of short beams. I doubt that any apply to your specific case. A complete solution requires FEA, however a real world solution can usually be found by looking at the point where the 30,000 N force is attached. If the immediate vicinity of the force attachment is strong enough, and the "rigid support" is strong enough, then the big solid block in between is usually strong enough. Note that I said "usually".

 

[Joe591]

This is what I was looking . I don't really feel qualified to do Fea, but i plugged this scenario into a FEA simulation and the average stresses throughout the member were significantly higher than my equations suggested they would be. I think you have explained why. Thanks for the link. I suppose equations have limits of applicability.

 

[jrmichler]

equations have limits of applicability

Very true. ALL equations, all simulations, all computer programs have limits of applicability. The challenge is to understand those limits, and the effect of those limits, on your problem.

 

[miltos]

You could start with some approximations (even extreme) and see how safe you are. Then you can go to more realistic assumptions. A good (and somewhat realistic but not necessary from the safe side) start is to consider an effective zone of the welding assuming a 45 degree angle from the hole to the welding and calculate the effective length of the welding.

PS Do you really have 30kN force at a 5mm hole?

 

[Joe591]

Thanks for your input. The point of this is how to go about analysing something that does not conform to basic theory. The dimensions are more or less made up. It's more of a conceptual problem and the conceptual solutions so far are more or less what I was looking for.