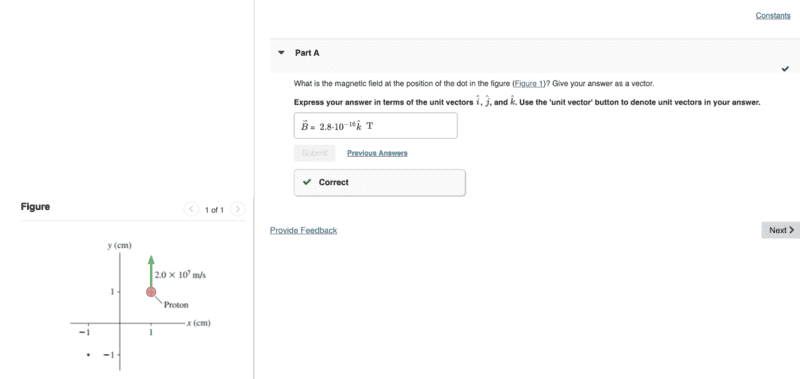
SUMMARY
The discussion centers on calculating the magnetic field generated by a proton moving with a specific velocity. The participants analyze the cross product of the velocity vector and the position vector, noting that the calculation involves the unit vectors i, j, and k. A key point raised is the ambiguity regarding the charge's sign and the necessity for a clear problem statement to facilitate understanding. The participants conclude that a clearer representation of the problem would enhance comprehension and accuracy in solving the magnetic field calculation.
PREREQUISITES
- Understanding of vector mathematics, specifically cross products.
- Familiarity with magnetic fields and their relationship to moving charges.
- Knowledge of unit vectors in three-dimensional space.
- Basic principles of electromagnetism, particularly the Lorentz force law.
NEXT STEPS
- Review the principles of the Lorentz force and its application in magnetic field calculations.
- Study vector cross product operations in three-dimensional space.
- Examine the effects of charge sign on magnetic field direction and magnitude.
- Learn how to formulate clear problem statements in physics to aid in problem-solving.
USEFUL FOR
Students and educators in physics, particularly those focusing on electromagnetism, as well as anyone involved in solving vector-related problems in physics.