How Are Angles Between Lines Related to Their Perpendiculars?
Click For Summary
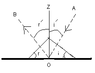
The discussion clarifies the relationship between the angles of two lines and their perpendiculars, emphasizing that the angle between two lines is not equal to the angles between their perpendiculars. Specifically, it states that the angle between two lines is the supplement of the angle between their perpendiculars, except when the lines are perpendicular themselves. The angles i and i' are congruent, as are angles r and r', due to their complementary nature in right triangles. The only scenario where the angles are equal is when the angle between the two lines is a right angle, forming a rectangle.
PREREQUISITES- Understanding of basic geometric principles, including angles and triangles.
- Familiarity with the concepts of complementary and supplementary angles.
- Knowledge of quadrilaterals, specifically rectangles and parallelograms.
- Ability to visualize geometric relationships between lines and their perpendiculars.
- Study the properties of complementary and supplementary angles in geometry.
- Explore the characteristics of quadrilaterals, focusing on rectangles and parallelograms.
- Investigate the geometric proofs related to angles formed by intersecting lines.
- Learn about the applications of angles in real-world scenarios, such as architecture and engineering.
Students of geometry, educators teaching geometric concepts, and professionals in fields requiring geometric analysis, such as architecture and engineering.
Similar threads
- · Replies 20 ·
- · Replies 12 ·
- · Replies 10 ·
- · Replies 9 ·
- · Replies 4 ·
- · Replies 59 ·
- · Replies 4 ·
- · Replies 7 ·
- · Replies 2 ·
- · Replies 11 ·