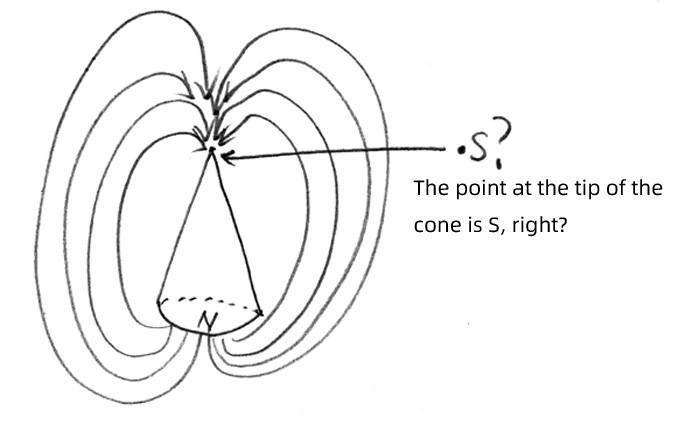
The distribution of poles in a tapered magnet, such as a conical magnet, can be effectively analyzed using Finite Element Method (FEM) modeling software. This approach allows for precise calculations of magnetic force and field lines, which do not concentrate at the apex as intuitively expected. A referenced FEM model provides a clear visual representation of these magnetic characteristics, enhancing understanding of tapered magnet behavior.
PREREQUISITESEngineers, physicists, and researchers interested in magnet design and analysis, particularly those working with tapered magnets and magnetic field modeling.
Looks like FEM modeling software is your best bet for finding magnetic force. Below is an example FEM model of a conical magnet that I found online. Note that the magnetic field lines don't concentrate at the apex nearly as strongly as in your hand sketch.vdance said: