How Are Triangle Altitudes and Inscribed Circle Radius Related?

[anemone]

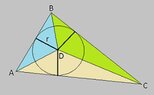
If $a_1,\,a_2,\,a_3$ are the altitudes of a triangle and $r$ is the radius of its inscribed circle, show that $\dfrac{1}{a_1}+\dfrac{1}{a_2}+\dfrac{1}{a_3}=\dfrac{1}{r}$.

---

Remember to read the http://www.mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to http://www.mathhelpboards.com/forms.php?do=form&fid=2!

 

[anemone]

Congratulations to the following members for their correct solutions::)

1. greg1313
2. lfdahl
3. kaliprasad

Solution from lfdahl:

Spoiler

View attachment 3915
The inscribed circle is the largest possible circle inside the triangle. Its center is located at the point where the three angle bisectors meet ($D$). The circle has the three sides of $\triangle ABC$ as tangents.

The area of the $\triangle ABC$ is the sum of the areas of the coloured triangles inside. The coloured triangles all have an altitude of length $r$ per definition of the inscribed circle.

$T_{ABC} = T_{ADB}+T_{BDC}+T_{CDA}= \frac{1}{2}ar+ \frac{1}{2}br + \frac{1}{2}cr = \frac{1}{2}(a+b+c)r$

Rewriting the above equation:

$\frac{1}{2}(a+b+c) = \frac{T_{ABC}}{r}$

Introducing the altitudes $a_1,a_2$ and $a_3$ of $\triangle ABC$ in the equation:

$\frac{\frac{1}{2}aa_1}{a_1}+\frac{\frac{1}{2}ba_2}{a_2}+\frac{\frac{1}{2}ca_3}{a_3} = \frac{T_{ABC}}{r}$$ \Rightarrow \frac{T_{ABC}}{a_1}+\frac{ T_{ABC}}{a_2}+\frac{ T_{ABC}}{a_3} = \frac{T_{ABC}}{r}$$ \Rightarrow \frac{1}{a_1}+\frac{ 1}{a_2}+\frac{ 1}{a_3} = \frac{1}{r}$.

Solution from kaliprasad:

Spoiler

let $x,\,y,\,z$ be the sides of triangle with corresponding altitudes $a_1$.$a_2$ and $a_3$ and area be A

so $xa_1 = ya_2 = za_3= 2A$

so

$\begin{align*}\dfrac{1}{a_1} + \dfrac{1}{a_2} + \dfrac{1}{a_3}&=\dfrac{x}{2A} + \dfrac{y}{2A} + \dfrac{z}{2A}\\&=\dfrac{2s}{2A}\\&=\dfrac{s}{A}\cdots(1)\end{align*}$

now because

$\begin{align*}r^2&=\dfrac{(s - x)*(s - y)*(s - z)}{s}\\&=\dfrac{s(s - x)*(s - y)*(s - z)}{s^2}\\&=\dfrac{A^2}{s^2}\end{align*}$

so $r = \dfrac{A}{s}$Putting the above in (1) we get the result.