How can I calculate the vacuum pressure in Y-junction?

[cajamarcus]

Hi, even though it seems so simple; I can't solve this since a few days and it's driving me crazy.

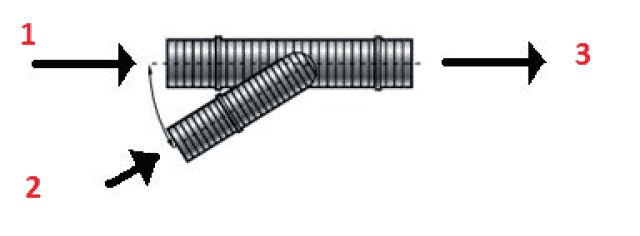
Flow gets inside the tube from point 1, it will create a vacuum, which will let a secondary flow inlet from point 2. Both flows will mix inside the tube, and get out of the junction from point 3. All the point ends are open to the ambient (so, the atmospheric pressure). The question is, what will be the static and dynamic pressures, as well as flow velocities in points 1, 2, and 3?

My basic assumption is to use Bernoulli equation and Continuity and Conservation of Mass. I am having trouble in using Bernoulli I guess.

in: Inlet
out: Outlet
P: Pressure
rho: Density
g: Gravitational acceleration
h: Height

Bernoulli Equation: P_static+P_dynamic+P_potential must be constant
Considering the fluid is water (incompressible), density will be constant.
P_in+1/2*rho*v_in²+rho*g*h_in=P_out+1/2*rho*v_out²+rho*g*ho_ut

considering that both the points are at the same elevation, we can ignore the potential pressure.
P_in+1/2*rho*v_in²=P_out+1/2*rho*v_out²

Most probably, my mistake comes at this point. Since there are 2 openings in inlet side, how should I integrate the pressures of point 1 and 2?

m: Mass flow rate
A: Crossectional area of the pipes
v: fluid velocities inside the pipes

Continuity and Conservation of Mass:
Considering the diameters of all 3 points are the same, areas are also same.
m₁+m₂=m₃
A*rho*v₁ + A*rho*v₂=A*rho*v₃
v₁+v₂=v₃

My assumptions are most probably wrong. Please correct me and help to find the right equations.

Thanks!

 

[DannySmythe]

While I can't answer your question, you may be interested in the discussion of the problem I was having with a Y adaptor.
See
Please explain curious behavior with my rainwater barrel

 

[OmCheeto]

While I can't answer your question, you may be interested in the discussion of the problem I was having with a Y adaptor.
See
Please explain curious behavior with my rainwater barrel

I was thinking the same thing.
But, I wouldn't hold your breath on a solution to this new "y" problem.
After almost two weeks, the following thread does not seem to be nearing a consensus: Mythbusters: Blow your own sail

I suspect the solution to that one also involves entrainment. Though, I'm not willing to do the experiment to prove or disprove it. Hence, why I haven't joined that discussion.

But this "y" problem looks like it can be solved empirically.
I may build a contraption, to test this.
But not this weekend, as I have appointments, with the river.

Empirical Evidence: A Definition
by Kim Ann Zimmermann | July 07, 2012 10:38am ET
​

Actually, thinking about it, I have all the necessary apparatuses to solve both problems.
Solving two problems with one experiment is always worthwhile.

[edit] A direct link to the
Please explain curious behavior with my rainwater barrel
thread.

 

[cajamarcus]

I am glad that some people are interested. I tried to solve it by a CFD software; but I am not satisfied with the results. I've got either a wrong result, or a result that I don't have any idea how it comes, where it comes.
Actually, I am just learning CFD, so don't trust my results on it. If anyone know those software good, it would be an easier alternative to experiment. Experimental or Empirical; any help is appreciated :)