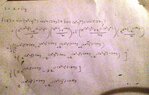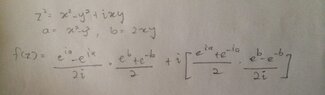How can I express f(z) in terms of z using exponentials?
- Context: MHB
- Thread starter aruwin
- Start date
-
- Tags
- Terms
Click For Summary
SUMMARY
The discussion centers on expressing the function f(z) in terms of z using exponentials. The user successfully derives that if z = x + iy, then z² = x² - y² + i(2xy), leading to the conclusion that f(z) = sin(z²). The user also notes that this method is faster than using exponentials but seeks clarification on how to express the function using exponentials. The relevant identities for sine involving complex numbers are highlighted, specifically sin(X + iY) = sin(X)cosh(Y) + i cos(X)sinh(Y).
PREREQUISITES- Understanding of complex numbers and their representation (z = x + iy).
- Familiarity with complex functions, specifically sine and its properties.
- Knowledge of hyperbolic functions, such as sinh and cosh.
- Basic algebraic manipulation of complex equations.
- Learn how to express complex functions using exponential forms, particularly Euler's formula.
- Study the derivation of sine and cosine functions in terms of complex exponentials.
- Explore the implications of using hyperbolic functions in complex analysis.
- Investigate the applications of complex functions in physics and engineering.
Students and professionals in mathematics, physics, and engineering who are working with complex analysis and need to understand the relationships between trigonometric and exponential functions.
Similar threads
- · Replies 9 ·
- · Replies 10 ·
- · Replies 5 ·
- · Replies 4 ·
- · Replies 3 ·
- · Replies 1 ·
- · Replies 24 ·
- · Replies 8 ·
- · Replies 17 ·