How can I solve double integrals with tricky limits and substitutions?

[ApeXaviour]

I was fine with these in class, tutorials etc. It's only since I found this in a past paper that I've had a problem with them.
\[ \int_0^1\! \int_{\sqrt{y}}^1 9\sqrt{1-x^3}\,dxdy.\] <br />

Nomatter what I substitute in under the sqrt sign I just can't get out the integral for x :(
I tried changing the limits so they run from x^2 to 1 for y and 0 to 1 for x..


I'm having similar trouble with this one...

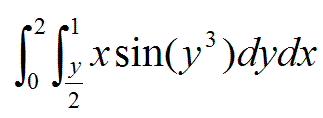
The Sin(y^3) here is what's getting me. Also tried changing the limits and substitution. No luck.. just ends up a big unsolvable mess for me

Thanks
Declan

 

[StatusX]

For the first one, if you interchange the limits, y will run from 0 to x^2, which will let you do the x integral by substitution. The second integral doesn't make sense as wriiten, but the same approach as for the first one will work if you meant for the inner integral to run from x/2 to 1.

 

[ApeXaviour]

Hmm.. you're right. I didnt even notice that about the second one. Re-checked the past exam papers and that's exactly how it's written though. Must be a missprint.

I obviously don't have the hang of changing these limits, thanks for your help I'll try wrap my head around that now..

 

[TD]

If you're having trouble finding new limits, a sketch of the graph will certainly help!