How can you make a free body diagram for someone running then sliding?

[amama]

Let's say you are riding a bike very fast, and then you sharply turn into a slide (where the bike is sliding perfectly sideways).

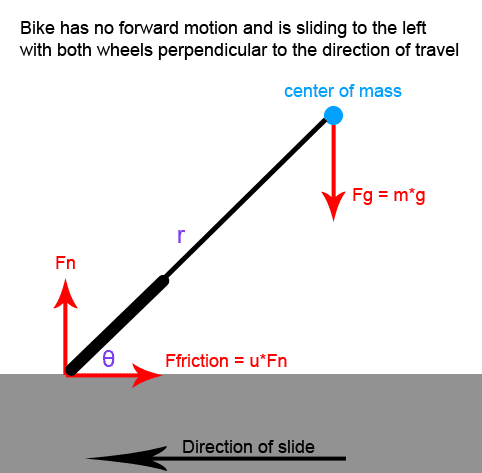
I'm trying to calculate the angle that the bike would be leaning at, but I'm having trouble creating the free body diagram.

Right now I have the normal force and friction force drawn where the wheels touch the ground. I also have the force from the weight drawn at the center of mass.

The approach I took is to calculate the torque around the wheel-contact point (pivot point) and set it equal to zero. However, right now, the only torque around the contact point is from the force of the weight, and there is nothing counteracting it, so the bike would fall. I would have guessed that the force of the friction would provide the force holding the bike up, but it doesn't provide any torque around the pivot point.

I'm guessing that I'm either missing a force or incorrectly locating the pivot point. Does anyone know where my error is?

 

[PeroK]

If the pivot point is the wheel, then that is accelerating. It's not a fixed point in any inertial reference frame. Instead, you could consider the torque about any fixed point on the ground.

 

[amama]

If the pivot point is the wheel, then that is accelerating. It's not a fixed point in any inertial reference frame. Instead, you could consider the torque about any fixed point on the ground.

Thanks for the response. I might need to dig out my textbook since I don't remember all the nuances of torque. But if I set the reference point on the ground, I still don't see where the force holding the weight up would come from. Wouldn't the torque from the friction force still always be zero?

I added a diagram.

 

[Lnewqban]

You may be able to keep a brief balance between the braking effect of the sliding tires and the negative acceleration of the center of mass.
The vertical distance between the contact patches of the tires and the combined center of mass of the bike-rider induces a brief CCW moment in your case.

The rate of change of momentum is equivalent to a instantaneous force and subsequent moment.
If at all possible, that balance would be very brief and precarious.

With not forward turning movement inducing a centrifugal force, the sliding bike and rider will hit the ground very quickly.

 

[256bits]

Thanks for the response. I might need to dig out my textbook since I don't remember all the nuances of torque. But if I set the reference point on the ground, I still don't see where the force holding the weight up would come from. Wouldn't the torque from the friction force still always be zero?

I added a diagram.

Just to give you a different perspective.
Take a broom, or yardstick, and balance it on a finger.
Now let it tip over a bit.
How much acceleration should your finger have so that the broom does not fall completely over.

 

[amama]

With not forward turning movement inducing a centrifugal force, the sliding bike and rider will hit the ground very quickly.

View attachment 293217

View attachment 293218

Another way to think of the problem would be to imagine someone doing the hockey stop on ice skates. They won't be vertical when they do it, instead they will be at an angle.



You can also do it rollerblading

 

[Lnewqban]

Note that there must be sufficient friction between skates and ice to induce the negative deceleration.
The lean angle balances forces and moments during braking time in such a way that the line of direction of the resultant force passes through the center of mass of the skater and the edge of the skates.

From own experience with motorcycles I can tell you that lack of friction force puts you on the ground surprisingly quick.

Please, see:
https://en.wikipedia.org/wiki/Impulse_(physics)

http://hyperphysics.phy-astr.gsu.edu/hbase/impulse.html

 

[PeroK]

Thanks for the response. I might need to dig out my textbook since I don't remember all the nuances of torque. But if I set the reference point on the ground, I still don't see where the force holding the weight up would come from. Wouldn't the torque from the friction force still always be zero?

I added a diagram.

Consider an object falling under gravity. Perhaps a rod of length $l$ falling in the horizontal position. The torque about one end of the rod would be $mg\frac l 2$. Should the rod rotate due to that torque? But, equally, there is the same torque about the other end of the rod.

The resolution is that as the rod is accelerating, then the angular momentum about either end of the rod is increasing - a change in angular momentum does not imply rotation. In this case, the accelerating linear motion of the centre of mass represents a change in angular momentum about any point not on the vertical line through the centre of mass.

In your case, if the normal force is also $mg$, then there is a torque and hence change in angular momentum about the point of contact. But, that change in angular momentum may represent the deceleration of the centre of mass about that point of contact - if the angle is just right.

PS although it is an unstable solution.