- #1
CollinsArg
- 51
- 2
Okay, hello there! I'm just beggining with an electricity course, and I saw this formula to claculate the Vrms :
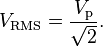 " Vrms=Vp/√2"... I'm trying to understand the origen of this formula, I see that I have to divide Vp%1,4142... but how do you explain a division with a decimal number..I mean If I divide 4apples into 2 I would have 2 groups of 2 apls. that's 2 as answer, but how can I divide 4 apples into 1,41? is there another way to explain this division?. Thanks.
" Vrms=Vp/√2"... I'm trying to understand the origen of this formula, I see that I have to divide Vp%1,4142... but how do you explain a division with a decimal number..I mean If I divide 4apples into 2 I would have 2 groups of 2 apls. that's 2 as answer, but how can I divide 4 apples into 1,41? is there another way to explain this division?. Thanks.
Last edited: