Discussion Overview
The discussion revolves around understanding decimal division in practical contexts, particularly in relation to the formula for root mean square voltage (Vrms) in an electricity course. Participants explore how to conceptualize dividing quantities, such as apples, by decimal numbers, and the implications of using irrational numbers in division.
Discussion Character
- Exploratory
- Conceptual clarification
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant questions how to explain dividing 4 apples by 1.41, seeking a practical analogy.
- Another participant suggests that dividing by 1.41 requires a different analogy, proposing the use of flagstones to illustrate continuous mathematics.
- Some participants argue that dividing by irrational numbers, such as √2, presents challenges that differ from dividing by integers.
- It is noted that dividing 4 apples into 1.4 groups could yield a mathematical answer, even if it seems illogical to think of fractional groups.
- Several participants discuss methods to eliminate decimals in division, such as multiplying both sides of the equation by powers of ten.
- One participant emphasizes that RMS is a special type of average relevant for sine waves, which complicates the analogy of dividing apples.
- Another participant points out that dividing quantities like liters of paint can be more intuitive than dividing discrete items like apples.
- There is a discussion about the nature of rational and irrational numbers, with some participants expressing discomfort with irrational denominators.
- One participant reflects on the broader implications of dividing by irrational numbers and the nature of numbers in mathematical contexts.
Areas of Agreement / Disagreement
Participants express a range of views on the topic, with no clear consensus on how to best conceptualize decimal division. Some agree on the challenges posed by irrational numbers, while others provide differing analogies and methods for understanding the division process.
Contextual Notes
The discussion highlights limitations in understanding decimal division, particularly when involving irrational numbers. Participants acknowledge the complexity of applying traditional division concepts to continuous quantities and the implications for mathematical reasoning.
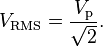 " Vrms=Vp/√2"... I'm trying to understand the origen of this formula, I see that I have to divide Vp%1,4142... but how do you explain a division with a decimal number..I mean If I divide 4apples into 2 I would have 2 groups of 2 apls. that's 2 as answer, but how can I divide 4 apples into 1,41? is there another way to explain this division?. Thanks.
" Vrms=Vp/√2"... I'm trying to understand the origen of this formula, I see that I have to divide Vp%1,4142... but how do you explain a division with a decimal number..I mean If I divide 4apples into 2 I would have 2 groups of 2 apls. that's 2 as answer, but how can I divide 4 apples into 1,41? is there another way to explain this division?. Thanks.