vcsharp2003
- 913
- 179
- Homework Statement
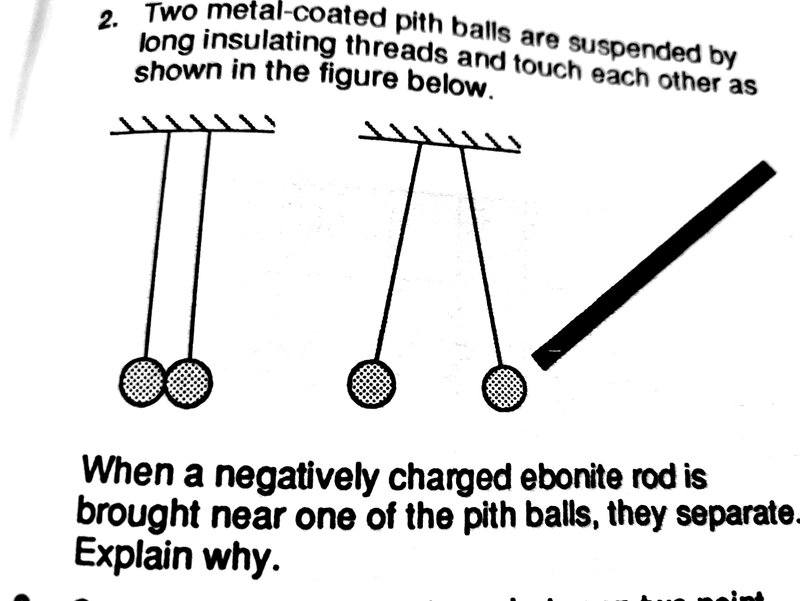
- Two metal coated pith balls are suspended by long insulating threads and touch each other as shown in diagram below. When a negatively charged ebonite rod is brought near one of the pith balls, they separate. Why does this separation occur?
- Relevant Equations
- ##F= \dfrac {k q_1 q_2} {r^2}##
Electrostatic induction where charges on a conductor separate so that one end has +ve charges and the other end has -ve charges when a charged object is brought near the conductor.
I used the concept of electrostatic induction, which would cause the charges in metal ball near the ebonite rod to have +ve charges on end next to rod and a -ve charge on the end touching the other ball.
What confuses me is how charges separate on the second ball. The only way these balls can separate is if ball 2 has -ve charges on end touching the ball 1. ( ball 1 is next to ebonite rod)
What I get after applying electrostatic induction.
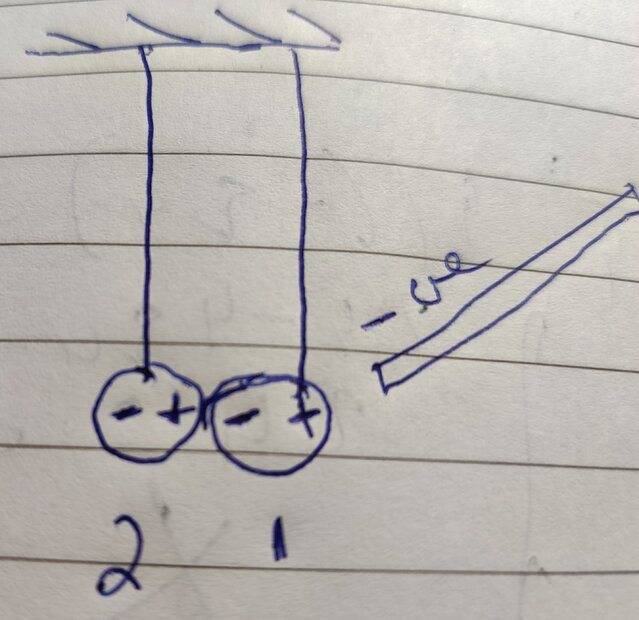
What confuses me is how charges separate on the second ball. The only way these balls can separate is if ball 2 has -ve charges on end touching the ball 1. ( ball 1 is next to ebonite rod)
What I get after applying electrostatic induction.
Last edited: