How Do Circles and Parallel Lines Interact in Geometry?

Click For Summary
SUMMARY

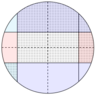
The discussion focuses on the interaction between circles and parallel lines in geometry, specifically addressing a problem involving area calculation. A user initially struggles with understanding how to determine the shaded and unshaded areas in a geometric figure. The solution involves recognizing that "cancelling" the dotted areas with their corresponding shaded areas results in a rectangle with an area of 32 cm², which represents the difference between the two areas. This method clarifies the relationship between the shapes involved.

PREREQUISITES
  • Understanding of basic geometric shapes, specifically circles and rectangles.
  • Familiarity with area calculation techniques in geometry.
  • Knowledge of the properties of parallel lines and their interactions with circles.
  • Ability to interpret geometric diagrams and visual representations.
NEXT STEPS
  • Study the properties of circles and their equations in coordinate geometry.
  • Learn about the area formulas for various geometric shapes, including circles and rectangles.
  • Explore the concept of geometric transformations, particularly translations and reflections.
  • Investigate the principles of geometric proofs involving parallel lines and transversal intersections.
USEFUL FOR

Students studying geometry, educators teaching geometric concepts, and anyone interested in enhancing their understanding of the interactions between circles and parallel lines.

wailingkoh
Messages
18
Reaction score
0
Hi all,

Please help. I am stuck with the question below and I have no clue how to solve:

View attachment 4573

Thanks for the help.
 

Attachments

  • wailingkoh01.jpg
    wailingkoh01.jpg
    26.5 KB · Views: 123
Mathematics news on Phys.org

Attachments

  • areas.png
    areas.png
    4 KB · Views: 129
Hi
Thanks for the reply. Do I solve it by fraction. Sorry, I am very lost with this question
 
8 multiply by 4 for 32 units square but I still won't get the full shaded and unshaded
 
You don't need them. "Cancelling" the dotted areas with their corresponding shaded areas leaves a dotted rectangle which is 32 cm. squared. That's the difference between the two areas.
 
Awesome!
I was so silly.

Thanks for the help.

This forum is great
 

Similar threads

MHB Find the area of the shaded region
  • · Replies 2 ·
Replies
2
Views
1K
MHB [ASK] A Line Intercepting A Circle
  • · Replies 4 ·
Replies
4
Views
1K
High School Inscribing a circle in an Oblique Square (Drafting)
  • · Replies 9 ·
Replies
9
Views
2K
MHB Finding the Center of a Circle
  • · Replies 3 ·
Replies
3
Views
1K
MHB Slope Intercept Equation with parallel
  • · Replies 2 ·
Replies
2
Views
1K
MHB Find the points of intersection of a line and a circle
  • · Replies 2 ·
Replies
2
Views
2K
Graduate How Does Non-Euclidean Geometry Differ from Euclid's Postulates?
  • · Replies 3 ·
Replies
3
Views
2K
High School Can You Solve This Simple Geometry Problem with Just a Ruler and Pencil?
  • · Replies 23 ·
Replies
23
Views
3K
Undergrad What Lobachevski meant by parallel lines
  • · Replies 5 ·
Replies
5
Views
3K
MHB Find the exact shaded area of the region in 4 overlapping circles
  • · Replies 1 ·
Replies
1
Views
3K