How do hydroelectric dams generate power?

[zzinfinity]

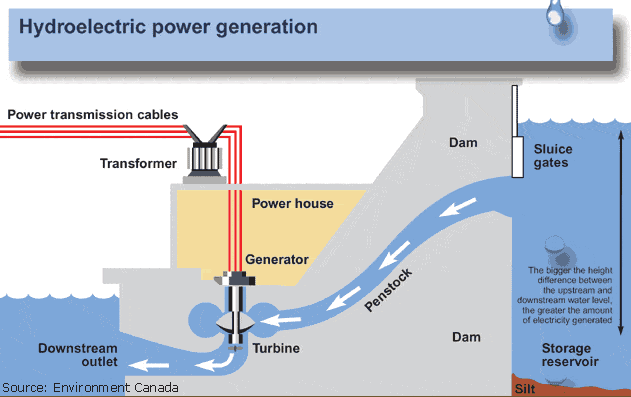
I don't quite understand how the law of conservation of energy applies to a hydroelectric dam, such as the one pictured below. My understanding is that the gravitational potential energy of the water in the reservoir will be converted to kinetic energy as it moves through the penstock. Where I'm confused is what happens to the energy of the water as it passes through the blades of the turbine? I see two possibilities.

1. Some of the kinetic energy of the water is transferred to the turbine causing it to spin. But if this is the case the water must slow down, meaning it would get backed up in the pipe? How can water have two different velocities when flowing through a pipe?

or

2. The water has the same speed both before and after it passes through the blades of the turbine. But if this is the case the water must have the same kinetic energy on both sides of the turbine, meaning no energy was transferred and thus no power can be generated.

Is there something in play here that I'm not seeing?

Your thoughts would be much appreciated. Thanks!

 

[Pengwuino]

Why would the water go back up the pipe if it slows down? When a car decelerates, it doesn't move backwards. Why would water?

 

[rcgldr]

For a reaction turbine, the energy transferred to the turbine corresponds to a drop in pressure of the water as it passes through the turbine. Water is almost incompressable, so since the mass flow rate is the same at every cross section of the penstock, turbine, and outlet (otherwise water would be accumulating), there's almost no change in speed or kinetic energy.

http://en.wikipedia.org/wiki/Reaction_turbine#Reaction_turbines

http://en.wikipedia.org/wiki/Francis_turbine

An impulse turbine involves a nozzle that directs a high speed flow at the blades of a spinning turbine, which change the direction and speed of the flow with little change in pressure, but that is not the type of turbine shown in the diagram of the first post of this thread.

 

[zzinfinity]

Hmm. I guess what I still don't understand is where the energy to turn the turbine comes from if the water doesn't loose any energy as it passes through the turbine. If the energy of the water remains unchanged, but the energy of the turbine increases, it seems like you're creating energy, which is not possible.

If the water never slows down it seems you could, in theory, put infinite turbines on a river, and produce an infinite amount of power. However from what I understand about energy it seems there must be an upper limit on the amount of electric power produced by a single river.

 

[chrisbaird]

The individual water molecules do slow down and loose kinetic energy as they strike the turbine, so the total energy of the system is conserved. But the average flow velocity of billions of interacting water molecules does not just depend on the individual molecules' velocities, but also on the pressure, which in turn depends on the pipe diameter and what is going on upstream. So as the individual molecules loose energy, this translates to a drop in pressure for a large volume of water instead of a drop in average flow velocity. Put another way, the entire system is filled with liquid water all bound together, so that is is better to think of a total column of water being heavy due to gravity and exerting pressure on the turbine, than on individual molecules striking the turbine.

 

[A.T.]

How can water have two different velocities when flowing through a pipe?

No problem, if the pipe changes in diameter.

 

[russ_watters]

Hmm. I guess what I still don't understand is where the energy to turn the turbine comes from if the water doesn't loose any energy as it passes through the turbine. If the energy of the water remains unchanged, but the energy of the turbine increases, it seems like you're creating energy, which is not possible.

It loses pressure energy, not kinetic energy. You're just confused about which type of energy you're dealing with.

 

[Delta Kilo]

It is not the kinetic but potential energy that matters. The water that goes through the turbine does not lose kinetic energy, but the water in the reservoir loses its potential energy.

Consider a cross-section of a pipe. The water on each side acts on another side with a force F = P S (P-pressure, S-area of the cross-section). If the water in the pipe is moving, this force produces work at a rate dW/dt = Power = P S V = P F (V-velocity, F-flow (in m^3/s). In an ordinary (horizontal) pipe with the same pressure at both ends, the work at both ends cancels out, but the pipe effectively transfers energy from one end to another (hydraulics). In case of turbine, the pressures before and after are different, so there is a net power = delta P x F. Pressure diferential is the usual delta P = rho g H.

 

[jschmidt]

In addition to the excellent points made by some of the previous posters, you also seem to not be taking into account that the outflow pipe is at a lower elevation than the turbine. In other words, gravity continues to pull on the water after it has gone through the turbine, slowed down, but then accelerates again as it 'falls' through the outlet pipe, yes?

 

[Naty1]

Interesting question!

The water that goes through the turbine does not lose kinetic energy, but the water in the reservoir loses its potential energy.

PE plus KE at the top of the penstock seems greater than the similar total at the bottom.
The difference is what is transferred to the turbine.

 

[Naty1]

In other words, gravity continues to pull on the water after it has gone through the turbine, slowed down, but then accelerates again as it 'falls' through the outlet pipe, yes?

The water can't slow down...unless the outlet pipe is bigger...otherwise water would accumulate...If the velocity at the bottom of the penstock is lower than at the top, where does all that volume go??

 

[Naty1]

wikipedia says:

Reaction turbines

Reaction turbines are acted on by water, which changes pressure as it moves through the turbine and gives up its energy.

which at superficially seems ok,,,

but if the turbine is removed, what happens to the energy otherwise used to power the turbine...it's obviously significant...

and if the pressure drops, how is the volume of water flow maintained??

 

[rcgldr]

reaction turbines ... pressure drop

but if the turbine is removed, what happens to the energy otherwise used to power the turbine

With the restriction of the turbine removed, the overall rate of flow through the penstock from the upper reservoir to the lower reservoir would increase.

 

[russ_watters]

but if the turbine is removed, what happens to the energy otherwise used to power the turbine...it's obviously significant...

If the turbine is removed, there is less restriction to flow and the entire column of water flows faster.

and if the pressure drops, how is the volume of water flow maintained??

What do you mean? Flow is maintained the way it always is: as a function of pressure drop from point A to point B. In the case of the hydroelectric turbine, there is virtually no restriction anywhere except the turbine, so the pressure loss everywhere else in the piping system is near zero.

 

[Naty1]

With the restriction of the turbine removed, the overall rate of flow through the penstock from the upper reservoir to the lower reservoir would increase.

If the turbine is removed, there is less restriction to flow and the entire column of water flows faster.

I had the same thought too...but could not reconcile it with this idea:

we INCREASE pressure at the bottom of the penstock,,,,, when the turbine is removed...and water flows faster? that seems counter intuitive...I am missing something here...

 

[A.T.]

I have a related question regarding "pressure energy" (as described http://hyperphysics.phy-astr.gsu.edu/hbase/press.html#ed") and the assumption of incomprehensibly:

Let's have water in a cylinder, with an increasing external force applied to the piston. If we assume incomprehensibly, the piston is not moving, so we are not doing any work. But the pressure and thus the pressure energy increases.

Is this where the assumption of incomprehensibly fails? If not: Where does the energy come from?

 

[russ_watters]

I had the same thought too...but could not reconcile it with this idea:

we INCREASE pressure at the bottom of the penstock,,,,, when the turbine is removed...and water flows faster? that seems counter intuitive...I am missing something here...

Who said removing the turbine increases the pressure at the bottom of the penstock?

 

[russ_watters]

I have a related question regarding "pressure energy" (as described http://hyperphysics.phy-astr.gsu.edu/hbase/press.html#ed") and the assumption of incomprehensibly:

Let's have water in a cylinder, with an increasing external force applied to the piston. If we assume incomprehensibly, the piston is not moving, so we are not doing any work. But the pressure and thus the pressure energy increases.

Is this where the assumption of incomprehensibly fails? If not: Where does the energy come from?

No, that concept assumes incompressibility.

The energy is potential energy. You haven't done any work on an incompressible fluid by pressurizing it; you've only gained the potential to do energy. That's what a reservoir above a hydroelectric dam is for! It only releases the energy when you open a valve and let the water flow out the bottom.

 

[A.T.]

Let's have water in a cylinder, with an increasing external force applied to the piston. If we assume incomprehensibly, the piston is not moving, so we are not doing any work. But the pressure and thus the pressure energy increases.

The energy is potential energy.

But usually you have to do work to increase the potential energy of something.

Just to make sure: I'm asking about pressure energy as defined here:
http://hyperphysics.phy-astr.gsu.edu/hbase/press.html#ed
Not about potential energy as defined here:
http://hyperphysics.phy-astr.gsu.edu/hbase/press.html#fpe

You haven't done any work on an incompressible fluid by pressurizing it; you've only gained the potential to do energy.

Not sure what "potential to do energy" means. My question is: Does the total energy of the fluid increase, when the force on the piston increases?

That's what a reservoir above a hydroelectric dam is for! It only releases the energy when you open a valve and let the water flow out the bottom.

That is potential energy due to position in a gravity field, which doesn't change for the fluid in my cylinder. I'm interested in the pressure energy.

 

[russ_watters]

Not sure what "potential to do energy" means.

Sorry, that should have been the potential to do work.

My question is: Does the total energy of the fluid increase, when the force on the piston increases?

I think it would have to depend on how the force is applied. If the force is applied by a weight being lifted onto the top of the cylinder, for example, then the total energy of the system has certainly increased. In the case of the hydroelectric dam, the water at the bottom gains the potential to do work by piling more water on top of it, just as if you had lifted a weight on top of a piston.

That is potential energy due to position in a gravity field, which doesn't change for the fluid in my cylinder. I'm interested in the pressure energy.

In this case, they are one and the same. Or if you prefer, one causes the other: At the bottom of a hydro reservoir, the pressure is equal to the weight of the fluid. That's why the equations are identical to each other. In your piston-cylinder example, the piston has to do the work, so only by seeing how it applies the pressure can we know if the whole system has gained potential energy. It could be a spring, compressed air, a weight, etc. The potential energy could be different for the same pressure, depending on how the force is applied. In a hydro dam, the force is applied by piling water on top of more water.

 

[A.T.]

Does the total energy of the fluid increase, when the force on the piston increases?

I think it would have to depend on how the force is applied.

But the fluid pressure energy depends only on the pressure, not where the force comes from. So the total energy of the fluid must increase, unless some other energy term of the fluid decreases.

If the force is applied by a weight being lifted onto the top of the cylinder, for example, then the total energy of the system has certainly increased.

I don't have to lift the weight. It can be already lifted hanging on a rope, barely touching the lid sealing a full cylinder. When I cut the rope, the weight looses no potential energy. But the pressure energy of the fluid increases. Where did the energy come from?

In this case, they are one and the same. Or if you prefer, one causes the other:

If potential energy & pressure energy are the same thing, then why are they represented by two separate terms in the Bernoulli Equation?
http://hyperphysics.phy-astr.gsu.edu/hbase/pber.html

 

[rcgldr]

PE plus KE at the top of the penstock seems greater than the similar total at the bottom. The difference is what is transferred to the turbine.

You left out a pressure term. Total energy for a volume of water = pressure x volume + PE + KE and is the same within the penstock until the water goes through the turbine (ignoring pressure losses due to friction with the penstock surfaces). The turbine extracts energy by reducing the pressure energy (pressure x volume), with little change to PE + KE, and total energy is reduced by the energy extracted by the turbine (plus losses to heat).

With the restriction of the turbine removed, the overall rate of flow through the penstock from the upper reservoir to the lower reservoir would increase.

If the turbine is removed, there is less restriction to flow and the entire column of water flows faster.

I had the same thought too...but could not reconcile it with this idea:
we INCREASE pressure at the bottom of the penstock,,,,, when the turbine is removed...and water flows faster?

If you remove the turbine, then the pressure just before where the turbine used to be is reduced, since the restriction is removed. The pressure just beyond where the turbine used to be is greater, also because the restriction removed. Without the turbine extracting energy and restricting the flow, the flow rate ends up faster without the turbine.

For comparason, imagine you have a hose, you turn on the tap, and water flows through the hose. If you partiallly block off the end of the hose, the pressure near the end of the hose increases and the flow rate decreases. If you remove the restriction at the end of the hose, the pressure at the end of the hose decreases and flow rate increases.

 

[Redbelly98]

With the restriction of the turbine removed, the overall rate of flow through the penstock from the upper reservoir to the lower reservoir would increase.

That's probably the key to the OP's confusion. The water doesn't slow down*, but it moves slower than it would without the turbine blades present.

*Assuming a constant conduit diameter.

 

[Naty1]

In the case of the hydroelectric turbine, there is virtually no restriction anywhere except the turbine, so the pressure loss everywhere else in the piping system is near zero.

So that from Wikipedia is wrong??

 

[russ_watters]

So that from Wikipedia is wrong??

I don't know what you are referring to. Could you provide the source article and quote please.

 

[russ_watters]

But the fluid pressure energy depends only on the pressure, not where the force comes from. So the total energy of the fluid must increase, unless some other energy term of the fluid decreases.

If there is a moving piston doing work, it absolutely matters!

I don't have to lift the weight. It can be already lifted hanging on a rope, barely touching the lid sealing a full cylinder. When I cut the rope, the weight looses no potential energy. But the pressure energy of the fluid increases. Where did the energy come from?

It came from you being sloppy about defining your system! If your fluid gained energy and the weight lost no energy, then you've just doubled your available energy in violation of conservation of energy.

If potential energy & pressure energy are the same thing, then why are they represented by two separate terms in the Bernoulli Equation?
http://hyperphysics.phy-astr.gsu.edu/hbase/pber.html

I'm talking about hydrostatic pressure. That's where the energy in a hydo dam comes from: http://hyperphysics.phy-astr.gsu.edu/hbase/pflu.html#fp

Do you see that the "potential energy" term in Bernoulli's and the hydrostatic pressure equation are the same?

 

[russ_watters]

The water doesn't slow down*, but it moves slower than it would without the turbine blades present.
*Assuming a constant conduit diameter. [emphasis added]

The bolded part isn't really needed. We're talking about a case 1 and case 2, not a change in velocity/flow rate as a parcel of water travels through the pipe. Restating the first sentence:

After removal of an obstruction, the velocity at any point is greater than at the same point before.

 

[A.T.]

If there is a moving piston doing work, it absolutely matters!

But the piston is not moving if the fluid is incompressible.

It came from you being sloppy about defining your system. If your fluid gained energy and the weight lost no energy, then you've just doubled your available energy in violation of conservation of energy.

And my question is, where exactly the error lies.

Do you see that the "potential energy" term in Bernoulli's and the hydrostatic pressure equation are the same?

Yes, but that doesn't change the fact, that the Bernoulli equation also contains another term additionally to "potential energy", called "pressure energy":

fluid_energy = pressure_energy + kinetic_energy + potential_energy

I don't quite see how you can claim that pressure_energy and potential_energy represent the same quantity here. Why would you count the same thing twice?

 

[rcgldr]

But the piston is not moving if the fluid is incompressible.

Incompressible fluids create dilemmas like this. Pressure can change without any work being done. I'm not sure why this was brought up, since incompressible fluids are just abstract concepts and don't actually exist.

Do you see that the "potential energy" term in Bernoulli's and the hydrostatic pressure equation are the same?

Yes, but that doesn't change the fact, that the Bernoulli equation also contains another term additionally to "potential energy", called "pressure energy":

fluid_energy = pressure_energy + kinetic_energy + potential_energy

The potential term in Bernoulli is related to gravitational potential (g h). Normally Bernolli's equation is written as energy per unit volume:

constant = pressure + 1/2 x density x velocity² + density x gravity x height

multiply this by some amount of volume and then you get

fluid_energy = pressure x volume + 1/2 x mass x velocity ² + mass x gravity x height

fluid_energy = pressure_energy + kinetic_energy + gravitational_potential_energy

 

[A.T.]

Incompressible fluids create dilemmas like this.

That was my assumption as well:

Is this where the assumption of incomprehensibly fails?

But Russ said:

No, that concept assumes incompressibility.

The potential term in Bernoulli is related to gravitational potential (g h).

That is how I understand it too. And pressure energy is something different, that is accounted for separately.

 

[russ_watters]

But the piston is not moving if the fluid is incompressible.

Yes, that's my point: In order for the water to do work, the piston has to move.

And my question is, where exactly the error lies.

It lies in the fact that you're double-counting the gravitational potential energy. In the hyperphysics page on Bernoulli's equation, it lists 3 pressures:

-Static pressure
-Velocity pressure
-Hydrostatic pressure

The pressure at the bottom of a hydro dam is hydrostatic pressure, but you're making the mistake that if you can measure it with a pressure gauge, it must be static pressure, so you're double-counting it. For your example of putting a weight on a volume of water, you've substituted that weight for the extra water column, changing nothing: you're still double-counting gravitational potential energy by using the static pressure term when it doesn't apply.

I don't quite see how you can claim that pressure_energy and potential_energy represent the same quantity here. Why would you count the same thing twice?

You shouldn't: the equation isn't doing that, you are.

That is how I understand it too. And pressure energy is something different, that is accounted for separately.

Yes. And in both the case of the hydro dam and the case of your piston-cylinder-weight, the [static] pressure energy is zero (if you consider the weight to still have its gpe).

 

[rcgldr]

In the hyperphysics page on Bernoulli's equation, it lists 3 pressures:
-Static pressure
-Velocity pressure
-Hydrostatic pressure

At this web page, I see the description potential energy per unit volume for the term ρ g h, not the term "hydrostatic pressure":

http://hyperphysics.phy-astr.gsu.edu/hbase/pber.html

Side note - the hyperphysics page also describes pressure as pressure energy, but pressure is energy per unit volume, the same as the other two terms in the equation.

hydrostatic pressure

Assuming I'm not misinterpreting this, hydrostatic pressure is the static pressure of a fluid due to gravity and is equal to ρ g h as described in this wiki article, but this is different than the ρ g h term used in Bernoulli's equation, which is a potential energy term:

http://en.wikipedia.org/wiki/Hydrostatic_pressure#Hydrostatic_pressure

Note that hydrostatic pressure increases with depth in a fluid, while the gravitational potential energy per unit volume term in Bernoulli's equation decreases with depth. Hydrostatic pressure corresponds to part or all of the static pressure term in Bernoulli's equation.