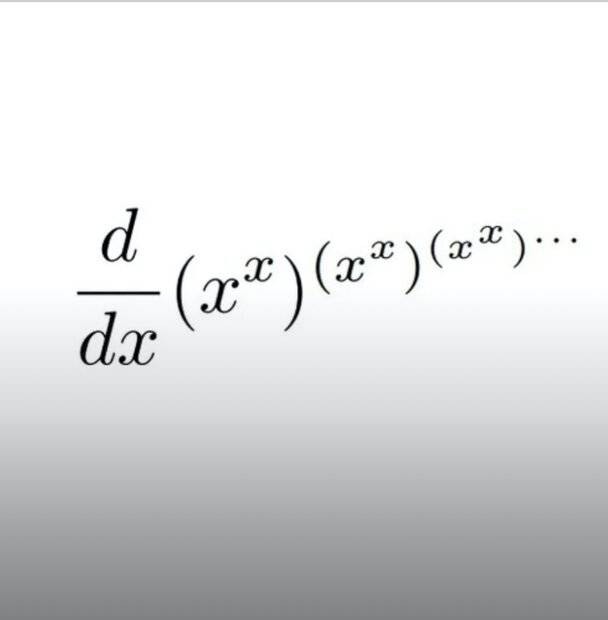SUMMARY
The discussion centers on computing the derivative of the function \( f(x) = ((x^x)^{(x^x)})^{(x^x)} \). Participants propose setting the equation \( f(x) = (x^x)^{f(x)} \) and derive a functional equation for \( f'(x) \). The Lambert W function is introduced as a tool for evaluating the derivative, leading to the conclusion that \( f'(x) = f^2(x) \frac{\ln x + 1}{1 - f(x) x \ln x} \). The domain of the function is debated, with consensus that it is well-defined for \( 0 < x \leq 1 \) and diverges for \( x > 1 \).
PREREQUISITES
- Understanding of derivatives and implicit differentiation
- Familiarity with the Lambert W function and its properties
- Knowledge of logarithmic identities and exponentiation rules
- Basic calculus concepts, particularly regarding function domains
NEXT STEPS
- Study the properties and applications of the Lambert W function
- Learn about implicit differentiation techniques in calculus
- Explore the behavior of functions defined by infinite exponentials
- Investigate the implications of function domains in calculus
USEFUL FOR
Mathematicians, calculus students, and anyone interested in advanced differentiation techniques, particularly those involving complex functions and the Lambert W function.