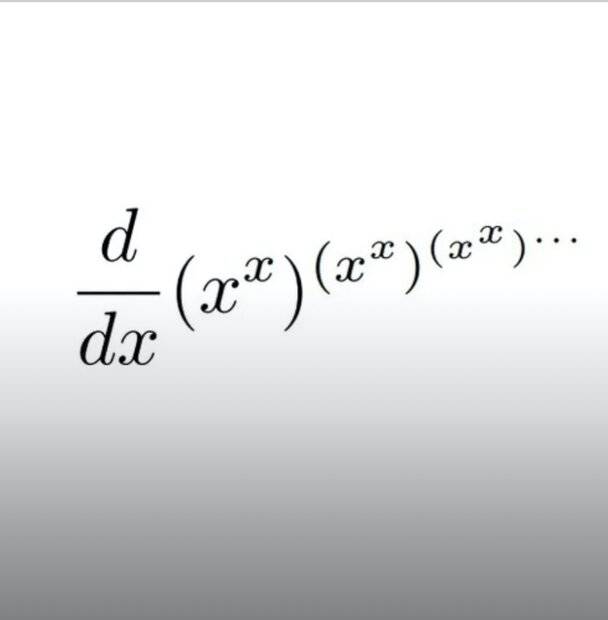Homework Help Overview
The discussion revolves around computing the derivative of a complex function defined as an infinite tower of exponentials, specifically \(((x^x)^{(x^x)^{(x^x)})}\). Participants are exploring the implications of this function's definition and its domain.
Discussion Character
- Exploratory, Assumption checking, Conceptual clarification
Approaches and Questions Raised
- Participants suggest setting the function as \(f(x) = (x^x)^{f(x)}\) and taking derivatives of both sides. There are questions about the function's domain and whether it is well-defined for certain values of \(x\). Some participants express uncertainty about the implications of the infinite exponentiation and its convergence.
Discussion Status
The discussion has evolved with various approaches being proposed, including the use of the Lambert W function. Some participants have acknowledged the need for clarity regarding the interpretation of multiple exponents and the conditions under which the function is defined. There is recognition of differing opinions and interpretations, but no explicit consensus has been reached.
Contextual Notes
Participants note that the function \(x^x\) is typically defined for \(x > 0\), and there is ongoing debate about the constraints on the domain of the original function due to its complexity. The discussion also touches on the conventions of exponentiation, which may affect the interpretation of the function.