How do I define a region in R3 with spherical/polar coords?

[Phantoful]

Homework Statement

Homework Equations

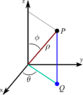
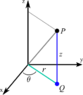
x^2 + y^2 + z^2 = r^2
Conversion equations between the three coordinate systems

The Attempt at a Solution

I tried to solve this problem using spherical/cylindrical coordinates from the beginning, but that wouldn't work so I started with cartesian. However, I couldn't find the boundaries for x or y, but I believe z is 0≤z≤2. Using either spherical and cylindrical, I found that 0≤θ≤2π. This is all I could extract on my own, and I don't know if it's even possible to convert without knowing φ (This is the angle from the z-axis). Am I approaching this wrong, or missing some information I should have extracted? (Or are my statements about z and theta wrong?)

 

[Gene Naden]

Hi, thanks for your inquiry. To do the spherical coordinates, rewrite the equation for the cone in terms of the polar angle theta (the angle from the z axis). You can then write an inequality for theta because all points in the region are inside the cone. Then write the equation for the sphere, in terms of the radius. You can then write an inequality for r because all points in the region are inside the sphere.

For cylindrical coordinates, you can write the equation for the cone as a relationship between rho (the distance from the z axis) and z. To be inside the cone, require an inequality in terms of rho and z. Then to do the sphere, write the radius r as a function of z and rho. You can then write an inequality where rho is less than a certain amount.

The azimuthal angle phi should not appear in any of your equations.

Good luck! Get back to me if you have more difficulty.

 

[Phantoful]

Hi, thanks for your inquiry. To do the spherical coordinates, rewrite the equation for the cone in terms of the polar angle theta (the angle from the z axis). You can then write an inequality for theta because all points in the region are inside the cone. Then write the equation for the sphere, in terms of the radius. You can then write an inequality for r because all points in the region are inside the sphere.

For cylindrical coordinates, you can write the equation for the cone as a relationship between rho (the distance from the z axis) and z. To be inside the cone, require an inequality in terms of rho and z. Then to do the sphere, write the radius r as a function of z and rho. You can then write an inequality where rho is less than a certain amount.

The azimuthal angle phi should not appear in any of your equations.

Good luck! Get back to me if you have more difficulty.

I'm a little confused with which symbols and angles you are talking about, my class uses a different set of symbols, and I think I actually also wrote them incorrectly in my original question (sorry!):

Spherical (ρ,θ,Φ):

Cylindrical, (r, θ, z):

In this notation, for Spherical I got 0 ≤ ρ ≤ 2 (top of the region W, correct?), and 0 ≤ θ ≤ 2π (goes all the way around x-y). For cylindrical I got 0 ≤ z ≤ 2 as well, and θ the same.

I'm not sure how I should be rewriting the equation for the cone in terms of Φ, the angle from the z-axis (do I use the coordinate conversion equations?), as well as rewriting the equation in terms of radius.

For the cylindrical part I didn't understand if you meant rho (ρ) as in actual distance from the z-axis or by angle. And again, how would you start rewriting the equations?

 

[Gene Naden]

Yes, well, you are using a different convention for the symbols. Here is my hint using the symbols the way you have defined them.
Your theta should not appear in the equations.
Yes, you use the coordinate conversion equations. I believe they are as below but you should compare to your notes.

SPHERICAL:
rho < 2, you have that right.
z=rho*cos(phi).
x^2+y^2 = rho^2 * (sin(phi)^2).
You should find a function f such that f(phi) < some constant. Phi is between 0 and pi/2 for this problem.
Because f increases with phi, this should give you an equation phi < another constant

CYLINDRICAL:
0 < z < 2 is not correct.
x^2+y^2=r^2

Try to work with that and please get back to me :)