How do I derive the formula for divergence using a prism-shaped volume?

[thatguy14]

Homework Statement

In deriving the formula
div v = $\frac{∂v_{x}}{∂x}$ + $\frac{∂v_{y}}{∂y}$ + $\frac{∂v_{z}}{∂z}$
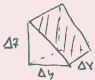
we used a rectangular solid infinitesimal volume; however, any shape will do (although the calculation gets harder). To see an example, derive the same formula using the prism-shaped volume shown (figure attached). This could be a volume element next to an irregular surface.

Homework Equations

Definition of divergence

div v = lim Δτ→0 $\frac{\int v \cdot da}{Δτ}$ where Δτ = small volume and the integral is a over a closed surface bound Δτ

The Attempt at a Solution

So I am having some issue with this question. A thing to note is that we are approximating the integral as just v$\circ$da where v is at some point on the surface. This is due to it being an infinitesimal volume.

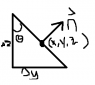
The main problem I am having is I think I am making a mistake on the top face somehow. If you look at figure 2 which is my crude drawing to represent n it is then

n = (cos$\theta$ jhat + sin$\theta$ khat)

So then for the top face if h = the slanted side
da = hΔx(cos$\theta$ jhat + sin$\theta$ khat)
=Δx(Δz jhat + Δy khat) because h can be expressed in terms of sin and cos of the other sides.

so then v dot da = v$_{y}$(x, y, z)ΔxΔz + v$_{z}$(x,y,z)ΔxΔy

hopefully so far so good. Now for the other faces

bottom

da = ΔxΔy (-khat direction)

v dot da = -v$_{z}$(x, y, z-$\frac{1}{2}$Δz)ΔxΔy

back(zx plane)

da = ΔxΔz

v dot da = -v$_{y}$(x, y-$\frac{1}{2}$Δy, z)ΔxΔz

so then when I put it all together and divide by Δτ = $\frac{1}{2}$ΔxΔyΔz

it almost looks like the definition of a derivative except I am left with a 1/2. What did I miss? Any help would be greatly appreciated and if you need me to clarify let me know.

 

[thatguy14]

Hey guys, I would really appreciate some help so if there is something I was unclear about let me know and I will try and clarify further thanks.

 

[TSny]

Note $f(x+a) \approx f(x) + f'(x)\:a$ for small $a$.

Likewise $f(x-a) \approx f(x) - f'(x)\:a$

Thus, how would you approximate $V_y(x, y-\frac{\Delta y}{2}, z)$?

 

[thatguy14]

So

=$\frac{[V_{y}(x,y,z)-V_{y}(x, y-\frac{1}{2}Δy,z)]}{\frac{1}{2}Δy}$
=V$_{y}$(x,y,z) - V$_{y}$(x,y,z) + $\frac{∂v_{y}}{∂y}$($\frac{1}{2}$Δy) / ($\frac{1}{2}$Δy)
=$\frac{∂v_{y}}{∂y}$

correct?

Sorry for the poor formatting I am still getting used to this latex stuff

 

[TSny]

Yes, that's correct.

 

[thatguy14]

Okay thank you again!