- #1
raymanmusic
- 31
- 1
How do I find deflection (displacement) in point C at the end of the beam? Answer is to be given in mm. There is a roller connection (only Fy) in B and an external pin in A (Fy and Fx). The module of elasticity and area moment of inertia is given.
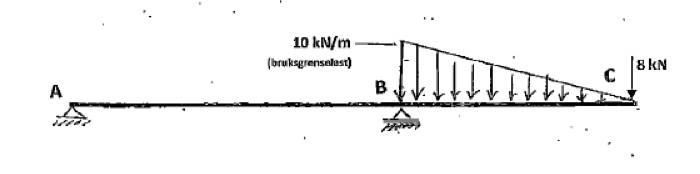
Relevant equations:
1. http://en.wikipedia.org/wiki/Deflection_(engineering)
2. http://www.advancepipeliner.com/Resources/Others/Beams/Beam_Deflection_Formulae.pdf
Here is a solution to a similar problem: https://dl.dropboxusercontent.com/u/11241083/beer_mecanica_4e_solucionario_c09_a.pdf
Relevant equations:
1. http://en.wikipedia.org/wiki/Deflection_(engineering)
2. http://www.advancepipeliner.com/Resources/Others/Beams/Beam_Deflection_Formulae.pdf
Here is a solution to a similar problem: https://dl.dropboxusercontent.com/u/11241083/beer_mecanica_4e_solucionario_c09_a.pdf
Last edited by a moderator: