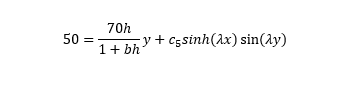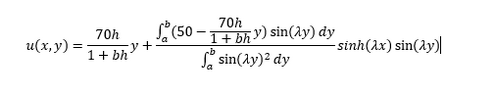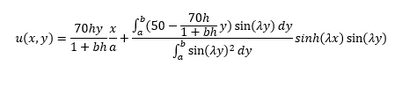How do I solve the Laplace equation using Robbin's Boundary Conditions?

[shreddinglicks]

Homework Statement

Equation

(d^2 u)/(dx^2 )+(d^2 u)/(dy^2 )=0

boundary conditions

u(0,y)=0
u(a,y)=50
u(x,0)=0
u^' (x,b)=-h[u(x,b)-70]

Relevant Equations

(d^2 u)/(dx^2 )+(d^2 u)/(dy^2 )=0

I've tried a few things. I did one method to try to accomplish the removal of the -70 in the derivative boundary condition. It came out as below. When plotting it however it gave a solution that didn't make sense.

 

[pasmith]

What is the boundary condition at $x = a$? What do you mean by the notation $u'$, since $u$ is a function of 2 varaibles? Do you mean $\frac{\partial u}{\partial x}$? Is $h$ a constant?

If that is correct, then I would set $$u(x,y) = \frac{70h}{1 + ah}x + v(x,y)$$ where $v$ satisfies $$\begin{split} v(0,y) = 0, \\ \frac{\partial v}{\partial x}(a,y) + hv(a,y) &= 0, \\ v(x,0) &= -\frac{70h}{1 + ah}x, \\ v(x,b) &= 50 - \frac{70h}{1 + ah}x. \end{split}$$

 

[shreddinglicks]

What is the boundary condition at $x = a$? What do you mean by the notation $u'$, since $u$ is a function of 2 varaibles? Do you mean $\frac{\partial u}{\partial x}$? Is $h$ a constant?

If that is correct, then I would set $$u(x,y) = \frac{70h}{1 + ah}x + v(x,y)$$ where $v$ satisfies $$\begin{split} v(0,y) = 0, \\ \frac{\partial v}{\partial x}(a,y) + hv(a,y) &= 0, \\ v(x,0) &= -\frac{70h}{1 + ah}x, \\ v(x,b) &= 50 - \frac{70h}{1 + ah}x. \end{split}$$

Yes, exactly as you said. du/dx and h is a constant.

I realized I made an error.

The conditions are actually

I'll fix it also on the original post.

It's what you have but y instead of x.

The problem is, this gives an answer where for all y when u(0,y)=0 when x should be zero, x does not equal zero.

The funny thing is if I manipulate the equation by multiplying the first term by x/a. I can plot a solution that makes sense.