SUMMARY
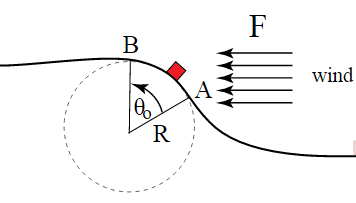
The discussion focuses on computing a line integral involving a dot product for a circular path, specifically represented as w = ∫_{a}^{b} \vec{f} · d\vec{s}. To evaluate this integral, one must first compute the dot product of the force vector \(\vec{f}\) with the differential line element d\vec{s}. For a circular path centered at the origin, the differential element is expressed as d\vec{s} = r dθ θ, where θ is the unit vector in the angular direction. The limits of integration correspond to the angles of the endpoints of the circular path.
PREREQUISITES
- Understanding of line integrals in vector calculus
- Familiarity with dot products in vector mathematics
- Knowledge of circular motion and angular coordinates
- Basic proficiency in calculus, particularly integral calculus
NEXT STEPS
- Study the properties of line integrals in vector fields
- Learn about the application of dot products in physics
- Explore circular motion and its mathematical representation
- Investigate the use of parametric equations in evaluating integrals
USEFUL FOR
Students of physics and mathematics, particularly those studying vector calculus and mechanics, as well as professionals working with line integrals in engineering and physics applications.