How Do You Calculate Acceleration in a Dual Pulley System with Unequal Masses?

[dibilo]

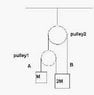
2 separate ropes A and B and 2 pulleys 1 and 2 are assembled together with 2 masses as shown. puley 1 is supported by rope B and each rope is tied separately to the heavier mass. Assuming ideal ropes and pulleys, what are the acceleration of each mass?.. (M moves 3 times as fast as 2M)..

the answers are g/11 and 3g/11 respectively but i am at a lost as to go about solving these sort of problems can someone please give me some ideal, hints or guidelines to start me off. thanks in advance. and sry for the really bad illustration

 

[Doc Al]

Welcome to PF!

Here are a few hints for you. First identify all the forces acting on the two masses and the two pulleys. Then apply Newton's 2nd law to each mass and to pulley #1. That will give you 3 easy equations with three unknowns: solve for the acceleration of the masses.

The real "trick" in these kinds of problems is to identify the acceleration constraints imposed by the connecting ropes. For example, in this problem if the acceleration of the 2M mass is "a" upwards, then the acceleration of the M mass is "3a" downwards. You seem to know that already, since you state "M moves 3 times as fast as 2M". (Did you figure that out or was it given?)

Why don't you take a crack at it with these hints and see how you do. Post your work and you'll get more help if you need it. Again, start by identifying the forces and drawing a separate diagram for each mass with the forces shown.

 

[dibilo]

this is all i figured out so far.
i know that on the left side of pulley 1, Mg-T=M(3a).. and pulley 1 will exert a force of 2T on the left side of pulley 2. 2M is being pulled by 2 upward forces one of them is T(force from M) and a downward force which is T-2Mg=2Ma, ... but the way the pulley was constructed is confusing me.

how do i know how much force is exerted on pulley 1(RHS) by 2M?

pls give more guidance on this.. off to school now.. thanks :)

 

[maverick280857]

Hi dibilo

Welcome to PF! Yes the real trick as our good ole Doc has suggested, is the application of constraints. To figure out the constraints you need a bit of visualization. But once you've done that, you're on your way to solving the force equations. The constraints yield acceleration of one body in terms of the other. Of course they're no magic tool to solve the problem and like everything, they must be used with discretion.

So I have a piece of advice for you: don't figure out which body is moving n times as faster (or slower) than which other body without thought...think about the problem first, write down the constraint equations and see if they make sense to you. Then confirm if the body in question is indeed moving the way you would expect it to (n times faster, slower, whatever) Then of course you can proceed to solve all the equations together to get what you want.

Enjoy physics

Cheers
Vivek

 

[maverick280857]

Constraints:

The key idea is that the overall length of the rope remains constant. Now try writing the equation of constraint. At this crucial step you should choose a consistent sign convention for positive and negative displacements and make sure you don't forget about it later for the sign of the accelerations will reveal which direction the body is moving in according to YOUR convention.

Now that you have the equation(s) of constraint, you can easily get the acceleration relationship can't you? Think over this and try applying all this to your problem...(I have deliberately not told you how to do this exactly...but I think this post, the previous and Doc's post all have enough hints to see you through the problem )

Cheers
Vivek

 

[TenaliRaman]

When we had mechanics in our course , i think i probably had the longest method for solving these kind of questions but it sure used to work.

I used the separate the system into different parts and analyse each part then i used to draw a diagram (a sort of a dependency diagram) to see as to how one sub-system affects the other(the links used to have info on the factors affected).Finally i used to finish off the problem.(ofcourse with more practice, i started doing it much faster).

So u may start with this technique,
1>separate the system into smaller subsystems. (in this case u can have 4 sub-systems ... 2 subsystems related to masses and 2 related to pulleys)
2>analyse each system .. (if possible have separate sheets for each and do it simultaneously ... if u don't know some values ... assign some variables to it).
3>try to see the dependencies betn the sub-systems. in this case it is easier RHS MASS<-->RHSPULLEY<--->LHSPULLEY<--->LHSMASS. (try to see what are the dependency factors) At this stage u should be able to determine as to why "(M moves 3 times as fast as 2M).." if u have come till here the 4th step is
4>finish the problem ... because once u have got that ... and did all the analysis i said ... u probably have everything u need to solve it.

whatever i said so far or DocAL said or vivek said are the samething ... but i just gave u a procedure that i followed to solve many mechanics problems and it *might* help you.

ofcourse i put out this thing since u wanted some guidelines on solving *such* problems.

ofcourse this post bears not much importance other than that :)
-- AI

 

[Doc Al]

this is all i figured out so far.
i know that on the left side of pulley 1, Mg-T=M(3a).. and pulley 1 will exert a force of 2T on the left side of pulley 2. 2M is being pulled by 2 upward forces one of them is T(force from M) and a downward force which is T-2Mg=2Ma, ... but the way the pulley was constructed is confusing me.

You need to approach the problem systematically. No shortcuts. First identify all the forces, giving them labels. Let T_1 be the tension in the cord around pulley 1 and T_2 be the tension in the cord around pulley 2.

So what forces act on the 2M mass? There are two upward forces: T_1 and T_2. And there is one downward force: the weight = 2Mg. (Note: "M" does not pull directly on "2M"! The only things touching 2M are the two ropes: they do the pulling, not M.)

Now it's time to apply Newton's 2nd law. But before we do, we need to adopt a consistent sign convention. Which way will the 2M mass accelerate? Let's say we have no idea (after all, that's part of what we are going to find out). So we guess: Let's assume it has an acceleration "a" upwards. And so we pick a sign convention in which up is positive. (If we guess wrong, "a" will turn out negative.)

So Newton's 2nd law tells us: T_1 + T_2 - 2Mg = 2Ma.

Make sense? So you tell me: What are the forces acting on the M mass? What's the magnitude and direction of the acceleration of the M mass? (Remember we are assuming that the 2M mass accelerates up with acceleration "a": be consistent.) Now apply Newton's 2nd law.

 

[dibilo]

ahh finally back from school, 1st of all thanks for all the replies. yup after some drawing of free body diagram, i got the same equation given by you.

if i assume 2M has an upward acceleration, then M will have a -ve acceleration (a') which gives me -Ma'=T3-Mg , whereby T3 is the upward force on the pulley

on pulley 1, i have an upward force which i named Ta and 2 downward ones. the left one which is connected to M which is T3 ,RHS=T1 which gives Ta=T3+T1

on pulley 2, 1 upward force (Tb) which is the resultant of, LHS, Ta and RHS, T2.
which gives Tb=Ta+T2

now i have a question, does the RHS of pulley 1 = to the LHS, as in T3=T1 which in turn means T3=T1=T2 ? if its so then i can solve it, but I've tried and failed to get a'=3a... which means i am wrong in that assumtion right? if that's the case could you pls give me some guidance on how do i get T1. thanks in advance.

 

[Doc Al]

if i assume 2M has an upward acceleration, then M will have a -ve acceleration (a') which gives me -Ma'=T3-Mg , whereby T3 is the upward force on the pulley

If 2M has an acceleration of "a" upward, then M will have an acceleration of "3a" downward. The tension is the rope attached to M is T_1. So: T_1 - Mg = M(-3a) = -3Ma

on pulley 1, i have an upward force which i named Ta and 2 downward ones. the left one which is connected to M which is T3 ,RHS=T1 which gives Ta=T3+T1

There are only two tensions in this problem: T_1 and T_2, as defined in my earlier post. (You do realize that the tension is equal on both ends of a rope going around an ideal pulley, right?) On pulley 1, the upward force is T_2, the downward force is 2T_1. So: T_2 = 2T_1.

on pulley 2, 1 upward force (Tb) which is the resultant of, LHS, Ta and RHS, T2.
which gives Tb=Ta+T2

Forget pulley 2.

now i have a question, does the RHS of pulley 1 = to the LHS, as in T3=T1 which in turn means T3=T1=T2 ? if its so then i can solve it, but I've tried and failed to get a'=3a... which means i am wrong in that assumtion right? if that's the case could you pls give me some guidance on how do i get T1. thanks in advance.

I find this puzzling. I thought you already figured out that "a'=3a"? Or did you just guess? I would figure out that relationship before writing equations.

Assuming you know the acceleration constraints, then you have three equations and three unknowns: T_1, T_2, and "a". Solve for a. This will tell you the acceleration of both masses: a & 3a.

On the other hand, if you don't know how to find the acceleration constraints, work on that first.

 

[dibilo]

yeah solved..thx to all. i was kindda stuck coz i didnt know an ideal pulley have forces even on both sides still a good lesson learned.

btw, a'=3a was given, but if its not, then how do i figure out myself? through visualization? or from the fact that there is 3 times the force acting on 2M, (on M=T1, on 2M=T1+T2=3T1).

 

[Doc Al]

how to find the acceleration constraint

btw, a'=3a was given, but if its not, then how do i figure out myself?

No need for mystic revelation or visualization.

Here's one way of working out the acceleration contraints. Find the relative acceleration between the masses and pulleys, one piece at a time. (If you don't know something, just give it a label and move on.) Again, I will start by assuming that mass B has an acceleration "a". Just for fun, I will assume mass B accelerates downward. (It doesn't matter.)

When I analyze the problem, here's what I find:
(1) acceleration of mass B with respect to pulley #2 = a (down)
(2) acceleration of pulley 1 with respect to pulley #2 = a (up)
(3) acceleration of mass A with respect to pulley #1= x (up)
(4) acceleration of mass B with respect to pulley #1= x (down)

Don't go any further until this makes sense. Now combine equations 2 & 3 to find the acceleration of mass A with respect to pulley 2:
(5) a' = x + a
Now combine equations 2 & 4 with 1:
(6) -a = a - x

Add these last two:
a' -a = 2a ===> a' = 3a (QED)

Make sense? Think this stuff over.

 

[maverick280857]

Hmm...all this stuff shouldn't look complicated. So I suggest (as I did earlier) that you should write the constraint using the fact that the length of the segment of the string is constant. Then differentiate both sides with respect to time to get the acceleration relationships. Plug them into Newton's laws and you're through. (Use the same +ve direction for accelerations and net forces). But please don't do it clerically--you are solving a physics problem..visualization is a must. How you do it now, is upto you as you have been given quite a few approaches.

 

[dibilo]

or from the fact that there is 3 times the force acting on 2M, (on M=T1, on 2M=T1+T2=3T1).

but is this method workable? like if i see that there is 2 or 3 times the force acting on a body 'b' w.r.t 'a' and i assume that 'a' have 2 or 3 times the acceleration w.r.t to 'b'

 

[Doc Al]

Hmm...all this stuff shouldn't look complicated.

It may look complicated when it's all written out, but it's not really.

So I suggest (as I did earlier) that you should write the constraint using the fact that the length of the segment of the string is constant.

That's exactly where these acceleration constraints come from!

Then differentiate both sides with respect to time to get the acceleration relationships.

I suspect you'll end up doing exactly what I did.

But please don't do it clerically--you are solving a physics problem..visualization is a must.

Good point. I was half-joking when I said "visualization" was not needed. Of course it's needed--it's essential. But don't try to look at the system of pulleys as one big mess and hope the answer jumps out at you. Break it down into managable pieces.

 

[Doc Al]

but is this method workable? like if i see that there is 2 or 3 times the force acting on a body 'b' w.r.t 'a' and i assume that 'a' have 2 or 3 times the acceleration w.r.t to 'b'

No, I don't think that method is workable. For one thing, how do you know how much force is on each mass until you apply Newton's law and figure it out? And another thing: The net force on A is 3/2 the net force on B. Is that obvious to you? It's not to me. (Of course, everything becomes obvious once you've figured it out. )

 

[maverick280857]

It may look complicated when it's all written out, but it's not really.

That's exactly where these acceleration constraints come from!

I suspect you'll end up doing exactly what I did.

Good point. I was half-joking when I said "visualization" was not needed. Of course it's needed--it's essential. But don't try to look at the system of pulleys as one big mess and hope the answer jumps out at you. Break it down into managable pieces.

Doc's right. Just keep the things simple...breakups help in physics ;-)