How do you Calculate Ampacity of a Conductor Geometry?

[BuddyBoy]

In practical applications it’s an assumed value born out from empirical evidence. You should have read that if you found it’s dependent on geometry, orientation, flow properties, etc… if it’s a smooth metallic plate material, it should be pretty much independent of the plate material itself(I believe).

Yea that's what I'm thinking. If only there was a "gold standard" for DC current for uninsulated copper bus bars. Then I can find the h by reversing the formula for h. Then use this value of h to calculate ampacity for nickel strips.

But it does seem h is near impossible to calculate.

It's been about 10 years since I took a COMSOL class and haven't used it sense, so I don't remember much, but is COMSOL able to simulate current through a strip and predicting it's surface temperature based on dimensions of the strip, it's resistivity, and ambient air temperature? Then I could simulate it and let the computer determine h??

 

[erobz]

Yea that's what I'm thinking. If only there was a "gold standard" for DC current for uninsulated copper bus bars. Then I can find the h by reversing the formula for h. Then use this value of h to calculate ampacity for nickel strips.

But it does seem h is near impossible to calculate.

It's been about 10 years since I took a COMSOL class and haven't used it sense, so I don't remember much, but is COMSOL able to simulate current through a strip and predicting it's surface temperature based on dimensions of the strip, it's resistivity, and ambient air temperature? Then I could simulate it and let the computer determine h??

Is there a true need for precision in this application? Many other aspects of the problem you are forming are approximated as well.

 

[BuddyBoy]

Is there a true need for precision in this application? Many other aspects of the problem you are forming are approximated as well.

No, if there's a rough estimate for h under natural convection, I would be glad to use it . I read somewhere between 5 and 25 W / (m^2 K). Is that as precise as I can get as a rough estimate? If so then I should just be conservative and chose the 5 value.

 

[erobz]

No, if there's a rough estimate for h under natural convection, I would be glad to use it . I read somewhere between 5 and 25 W / (m^2 K). Is that as precise as I can get as a rough estimate? If so then I should just be conservative and chose the 5 value.

What are the conditions like around the conductor? Still air, steady breeze, etc… if you assume a lower convection coefficient you get increased conductor temps, if assumed higher the converse is expected. It might be all that is practical-worst case scenario.

 

[BuddyBoy]

What are the conditions like around the conductor? Still air, steady breeze, etc… if you assume a lower convection coefficient you get increased conductor temps, if assumed higher the converse is expected. It might be all that is practical-worst case scenario.

For still air.

I was thinking of in terms of the equation, the current is directly proportional to the square root of h. So as h gets larger so does the current, and as it gets smaller so does the current. So I was thinking for a "safety" factor, I would pick the lowest value for h if there is some range and uncertainty in it's value, resulting in less current going through the conductor and therefore less surface temperature of the conductor.

Looking at your explanation though, it seems my thoughts process above is wrong, but I'm not sure how!

Thanks for all the help! I really appreciate it!

 

[erobz]

For still air.

I was thinking of in terms of the equation, the current is directly proportional to the square root of h. So as h gets larger so does the current, and as it gets smaller so does the current. So I was thinking for a "safety" factor, I would pick the lowest value for h if there is some range and uncertainty in it's value, resulting in less current going through the conductor and therefore less surface temperature of the conductor.

Looking at your explanation though, it seems my thoughts process above is wrong, but I'm not sure how!

Thanks for all the help! I really appreciate it!

I was referring to the temperature of the conductor. If the convection coefficient goes down the current must also go down, else the critical temperature for the conductor could be exceeded. We are basically saying the same thing. I'm speaking in terms of the physics, you are speaking in terms of the equation for $I$ as far I can tell.

 

[BuddyBoy]

I was referring to the temperature of the conductor. If the convection coefficient goes down the current must also go down, else the critical temperature for the conductor could be exceeded. We are basically saying the same thing. I'm speaking in terms of the physics, you are speaking in terms of the equation for $I$ as far I can tell.

Thanks. So I found the formula for how to calculate the value of h for a vertical and horizontal plate.
I'm getting that a 10 mm wide and 0.1 mm thick nickel strip can accept 6.57 A horizontally and 6.98 A vertically, with a surface temperature of 60 deg C for the nickel and 30 deg C ambient air.

The formula is a bit to difficult to write out on this forum, at some point I will try and put it here, and there's some conditional values when to use which formula over the other.

Now another question I have, representing a use case, of the nickel strip in a battery box without fans. Does natural convection still apply? Most battery boxes has holes for connectors, exposing the inside of the battery box to ambient air temperature. So it's not a completely enclosed space, but a very large percentage of it is.

 

[erobz]

Now another question I have, representing a use case, of the nickel strip in a battery box without fans. Does natural convection still apply? Most battery boxes has holes for connectors, exposing the inside of the battery box to ambient air temperature. So it's not a completely enclosed space, but a very large percentage of it is.

Yeah, but it becomes a system of transfers if the box is small. Heat is transferred from the conductor to the air contained in the enclosure, which is then conducted through the enclosure to the air surrounding the enclosure. This has the effect of raising the temperature of the conductor w.r.t to a conductor in a large “open” environment. Dimensions/thermal conductivity(new variables are obviously fine) for the material of the enclosure are needed to go anywhere with an analysis.

It’s a fairly straight forward extension of the problem when the systems are at steady state conditions because the power $I^2 R$ must be transferred across each boundary before it exits to the surroundings.

 

[BuddyBoy]

Yeah, but it becomes a system of transfers if the box is small. Heat is transferred from the conductor to the air contained in the enclosure, which is then conducted through the enclosure to the air surrounding the enclosure. This has the effect of raising the temperature of the conductor w.r.t to a conductor in a large “open” environment. Dimensions/thermal conductivity(new variables are obviously fine) for the material of the enclosure are needed to go anywhere with an analysis.

It’s a fairly straight forward extension of the problem when the systems are at steady state conditions because the power $I^2 R$ must be transferred across each boundary before it exits to the surroundings.

So the whole idea of finding the heat transfer of something like a battery box has got me thinking about finding the h values for a nickel strip.

In this equation

$$\dot{Q} = hA(T_{S}-T_{A})$$
h is a different value for each surface
A is a different value for each surface

This results in a dot product between the h values, and their respective areas.

Looking online the h value for a flat horizontal or vertical plate can be calculated via this formulas:

I played around with these formulas. Assuming that the nickel strip was not "floating" and one of the L*W surface areas was on some other flat surface (i.e., "the bottom"). Result in five different surfaces exposed to the ambient air.

Should I find the h value for each of the five exposed surfaces and consider them in calculating the current as a series of horizontal and vertical planes? Or do the formulas in the snap shot above already take this into consideration? Meaning what is the definition of a "plate"? I tried to find the derivation of these formulas, to see if it would aid in my understanding of how "plate" is defined, but didn't have any luck. At some thickness is my "plate" no longer considered a plate because it's to thick? I understand that I may be able to make the engineering estimation that the thickness may be considered insignificant, but I get different values for the current in the five surface analysis if I consider all five surfaces, vs only the one LW surface that is exposed to ambient air conditions.

Regardless, making the estimation that the thickness is insignificant and should not be considered, may not be an "option" but "required" to use the formulas to find h values for a flat plate? Meaning these formulas are inaccurate if you don't make this assumption? In order to use the formulas, you only consider the one LW surface.

Certainly for a battery box, the thickness should not be disregarded as insignificant, but for a nickel stirp they should be?

The other conceptional question I have, is "stacking" strips is common practice to reduce the overall resistance to allow for more current flow. If I have a 0.1 mm x 10 mm x 50 mm strip, and I calculate the ampacity current to be X amps given temperature desires, would "stacking" two identical strips of these dimensions on top of each necessarily give me 2*X amps at the same temperature desires?

Playing around with the numbers in the formulas:
If a strip with thickness t produces X current at given temperature conditions, and stacking N identical strips on top of each other:

1. If we consider this stack to be a new strip of equal dimensions except with N*t thickness, it produces a MUCH SMALLER number for the current then if you consider option 2
2. If we consider stacking N identical strips to result in a current of N*X current, than this produces a MUCH HIGHER number for the current than if you consider option 1

I'm not sure which method is correct above, 1 or 2. Intuitively, I would suspect Option 2 and Option 1 to agree and give the same values, but they don't. I wonder if this is the case, because stacking N strips on top of each other is no longer considered a "plate".

 

[erobz]

h is a different value for each surface
A is a different value for each surface

Yes, they can be different. I guess the box must be different in $A$, but its not a real issue- another variable.

That formula will only apply for the convection boundaries, across the box is a conduction boundary. just pretend heat is conducted across the walls and not up them in this portion. You will use what you know about $\frac{dT}{dx}$ for the plane wall.

Should I find the h value for each of the five exposed surfaces and consider them in calculating the current as a series of horizontal and vertical planes?

It's tied to the fluid mechanics, if the fluid mechanics of the flow around the plate become complex because of the geometry of the object in a flow, the heat transfer by convection does too. They are linked through the velocity boundary layer.

My opinion: Get an overview solution of the total heat transfer problem first. Drop all this finding $h$ stuff at least temporarily. Once you get the overall picture, you can focus on the fine details if it interests you - I'm not saying you'll find an answer, but you are free to torture yourself with it.

Or do the formulas in the snap shot above already take this into consideration? Meaning what is the definition of a "plate"? I tried to find the derivation of these formulas, to see if it would aid in my understanding of how "plate" is defined, but didn't have any luck. At some thickness is my "plate" no longer considered a plate because it's to thick?

Probably would have some issues - this is for the reason mentioned above , complex flow around the object, complex heat transfer.

I understand that I may be able to make the engineering estimation that the thickness may be considered insignificant, but I get different values for the current in the five surface analysis if I consider all five surfaces, vs only the one LW surface that is exposed to ambient air conditions.

let just assume low average $\bar{h}$ for the problem to get through it with the surrounding enclosure.

Certainly for a battery box, the thickness should not be disregarded as insignificant, but for a nickel stirp they should be?

Great, you need the thermal conductivity of the material the enclosure is made of and its thickness.

The other conceptional question I have, is "stacking" strips is common practice to reduce the overall resistance to allow for more current flow. If I have a 0.1 mm x 10 mm x 50 mm strip, and I calculate the ampacity current to be X amps given temperature desires, would "stacking" two identical strips of these dimensions on top of each necessarily give me 2*X amps at the same temperature desires?

I don't know for sure. For starters, you get half the resistance. Did you double the surface area exposed to the fluid?

You are trying to solve too many problems at once. Focus on the task at hand. Find the temperature of the conductor in the box given constant averaged $\bar{h}$, thermal conductivity of enclosure material $k$, the box thickness $\ell$ and the surface area of the box $A_{box}$.

At steady state there is no thermal energy accumulating in the system, hence the power $I^2R$ passes through each boundary without any of it being captured (if you will) by the stuff in between boundaries. Three of those are convection boundaries, and one of them a conduction boundary. Do you know how to find the steady state temperature of your conductor as a function of $I$?

 

[BuddyBoy]

Thanks for the reply!

At steady state there is no thermal energy accumulating in the system, hence the power $I^2R$ passes through each boundary without any of it being captured (if you will) by the stuff in between boundaries. Three of those are convection boundaries, and one of them a conduction boundary.

This is very perplexing to me! I'm looking through a textbook of a heating duct, and they also don't include the sides. Meaning in this picture, the two surface areas that would be calculated via $w*H**$ are ignored.

In the example solution they ignore those surface areas. In this example they find each h value for the surface areas involved. In the example above, it makes sense because the duct is open at two ends, and there is nothing physically there. But in my nickel strip example, I have physical metal on these sides. But in the nickel strip example, the current flows through the strip and is not trapped within the material. So the surface areas parallel to current flow are not considered.

Convection boundaries in my nickel strip example = 2Lt and LW
Conduction boundary is = LW

Do you know how to find the steady state temperature of your conductor as a function of I?

Given what you pointed out about there only being three surfaces which convection is to be considered, I can find the steady state temperature difference of the surface and the ambient air. I also need to consider the conduction boundary. Assuming that $h$ is the same for each surface.

Assuming that the strip rests along the "bottom" of a rectangular box, which sits on a table

Convection $\dot{Q} = h A (T_{S} - T_{\infty})$
Conduction $\dot{Q} = \frac{k}{t}A(T_{S} - T_{2})$
$S$ is Strip
$T$ is Table
$B$ is Box

$$\dot{Q_{S}} = \bar{h} A_{S} (T_{S} - T_{B}) + \frac{k_{B}}{t_{B}}A_{BS}(T_{S} - T_{B})$$
$$\dot{Q_{S}} = I_{A}^{2} R$$
$$R = \frac{\rho\;L}{W\;t}$$
$$\dot{Q} = I_{A}^{2} \frac{\rho\;L_{S}}{W_{S}\;t_{S}}$$
$$A_{S} = 2L_{S}t_{S} + W_{S}L_{S} = L_{S}(2t_{S} + W_{S})$$
$$A_{BS} = L_{S}W_{S}$$
$$I_{A}^{2} \frac{\rho\;L_{S}}{W_{S}\;t_{S}} = \bar{h}*L_{S}(2t_{S} + W_{S})(T_{S} - T_{B})+ \frac{k_{B}}{t_{B}}L_{S}W_{S}(T_{S} - T_{B})$$
$$I_{A}^{2} \frac{\rho}{W_{S}\;t_{S}} = \bar{h}(2t_{S} + W_{S})(T_{S} - T_{B})+ \frac{k_{B}}{t_{B}}W_{S}(T_{S} - T_{B})$$
$$I_{A}^{2} \frac{\rho}{W_{S}\;t_{S}} - \frac{k_{B}}{t_{B}}W_{S}(T_{S} - T_{B}) = \bar{h}(2t_{S} + W_{S})(T_{S} - T_{B})$$
$$(T_{S} - T_{B}) = \frac{1}{\bar{h}(2t_{S} + W_{S})}\;(I_{A}^{2} \frac{\rho}{W_{S}\;t_{S}} - \frac{k_{B}}{t_{B}}W_{S}(T_{S} - T_{B}))$$

My new equation for the ampacity of the conductor becomes:
$$I_{A}^{2} \frac{\rho}{W_{S}\;t_{S}} = \bar{h}(2t_{S} + W_{S})(T_{S} - T_{B})+ \frac{k_{B}}{t_{B}}W_{S}(T_{S} - T_{B})$$
$$I_{A}^{2} = \frac{W_{S}t_{S}}{\rho}(\bar{h}2t_{S} + W_{S})(T_{S} - T_{B})+ \frac{k_{B}}{t_{B}}W_{S}(T_{S} - T_{B}))$$
$$I_{A} = \sqrt{\frac{W_{S}t_{S}}{\rho}}\sqrt{(\bar{h}2t_{S} + W_{S})(T_{S} - T_{B})+ \frac{k_{B}}{t_{B}}W_{S}(T_{S} - T_{B}))}$$

Which is independent of $L$ if $h$ is provided numerically to you and you assume each surface area of the conductor has the same $h$ value.

Do these equations look correct?

Thank you for all the help!

Once I narrow down the equation, I can consider the heat transfer of the box to ambient air.

For conduction, is the A term the area at which the nickel strip comes into contact with the box, or the whole surface area of the plane that comes into contact with the nickel strip? I guess I had just assumed it was the surface area of the stirp L*W that came into contact with the "bottom" of the box? But I'm not sure if it should be the surface area of the bottom of the box L_B * W_B?

I'm thinking that I don't know the temperature of the box. But can I come up with the heat transfer equation of the box, and assume that the number of watts transferred by the strip within the box, is also the same number of watts transferred by the box to the ambient air? I can then come up with a equation for the temperature within the box, maybe?

 

[erobz]

You have to make some decisions about how you are handling things in this scenario. How big is this box surrounding the conductor in comparison to the conductor?

 

[BuddyBoy]

You have to make some decisions about how you are handling things in this scenario. How big is this box surrounding the conductor in comparison to the conductor?

View attachment 356551

That's a great picture!

Thanks, I believe that there is to many unknown variables here?
I know the dimensions of the strip.
I know the ambient air temperature.
I can come up with a formula for the temperature of the strip.

Oh wait a second, the temperature of the air within the box is the same temperature of the strip $T_{2}$? I was assuming that they would be different. But if they are the same. Than this might open some DOORS to calculating Convection of the battery box. I just want to be sure here that they are the same. Would defiantly make things easier.

I was also wondering I know you had mentioned that the surface areas perpendicular to the flow of air should not be considered for convection calculations. Is there anyway you could elaborate as to why this is the case? This is very perplexing to me.

I understand in the example above of a long air duct, that the surface areas perpendicular to the flow of the air (i.e. both wxH or 0.75 mm x 0.3 mm surface areas) should not be considered in convection calculations, because the duct is open on both ends, so there's physically no material there, and is likely connected to some other duct.

However in the case of my nickel strip I have physical material there, the green highlighted portion below. For example it's not a hollow rectangular box.

Nickel strips are commonly used in battery connections. Current still flows along the length of the strip, but it's more of like this
Case 1:

Where the red boxes are batteries or "the rest of the circuit". I'm not trying to perform this calculation or anything at this point with regards to "the rest of the circuit". Just trying to assess if the the two green surfaces should still not be considered in convection calculations if "the rest of the circuit" is connected in this way, as opposed to directly in contact with the two green surfaces (width times thickness) like below
Case 2:

Meaning that in both pictures with red boxes, where the red boxes represent "the rest of the circuit" and some other electrically conductive pieces, I do not consider the two green surfaces (length times thickness) in both situations? I can see in Case 2 I literally have some other item in full contact with the green surfaces, so therefore no convection occurs on these surfaces. But I'm unsure about Case 1.

I really do appreciate the help on this topic!

 

[erobz]

That's a great picture!

Thanks!

Oh wait a second, the temperature of the air within the box is the same temperature of the strip $T_{2}$? I was assuming that they would be different.

No, They are different. $T_1$ is the ss temp of the strip. We neglect thermal gradients in this body because its a relatively thin metallic substance with a high thermal conductivity. We assume that everywhere in the strip is uniformly $T_1$. There must be a temperature differential for heat to be transferred. Hence the surrounding air ( just outside of the convection boundary layer between it and the conductor ) in the box is $T_2$.

But if they are the same. Than this might open some DOORS to calculating Convection of the battery box. I just want to be sure here that they are the same. Would defiantly make things easier.

Its more accounting.

I was also wondering I know you had mentioned that the surface areas perpendicular to the flow of air should not be considered for convection calculations. Is there anyway you could elaborate as to why this is the case? This is very perplexing to me.
View attachment 356627
I understand in the example above of a long air duct, that the surface areas perpendicular to the flow of the air (i.e. both wxH or 0.75 mm x 0.3 mm surface areas) should not be considered in convection calculations, because the duct is open on both ends, so there's physically no material there, and is likely connected to some other duct.

However in the case of my nickel strip I have physical material there, the green highlighted portion below. For example it's not a hollow rectangular box.
View attachment 356628
Nickel strips are commonly used in battery connections. Current still flows along the length of the strip, but it's more of like this
Case 1: View attachment 356630
Where the red boxes are batteries or "the rest of the circuit". I'm not trying to perform this calculation or anything at this point with regards to "the rest of the circuit". Just trying to assess if the the two green surfaces should still not be considered in convection calculations if "the rest of the circuit" is connected in this way, as opposed to directly in contact with the two green surfaces (width times thickness) like below
Case 2: View attachment 356632
Meaning that in both pictures with red boxes, where the red boxes represent "the rest of the circuit" and some other electrically conductive pieces, I do not consider the two green surfaces (length times thickness) in both situations? I can see in Case 2 I literally have some other item in full contact with the green surfaces, so therefore no convection occurs on these surfaces. But I'm unsure about Case 1.

I really do appreciate the help on this topic!

It's about the boundary area. Imagine it is a thin film, heat is transferred across it, and in the direction of flow. We ignore this last part, that's why $h$ changes along the length. We are hand waiving that away. As for the open duct, the flow entering/exiting does not have a convection boundary with itself...it requires relative motion.

As for the green area, whatever you want to do with it. In the case of a solid conductor the flow which carries heat away would hit it...relative motion. BUT its a pretty tiny area, its most likely not worth the trouble of factoring it in unless you want to keep options open for geometry changes.

 

[BuddyBoy]

Thanks!

No, They are different. $T_1$ is the ss temp of the strip. We neglect thermal gradients in this body because its a relatively thin metallic substance with a high thermal conductivity. We assume that everywhere in the strip is uniformly $T_1$. There must be a temperature differential for heat to be transferred. Hence the surrounding air ( just outside of the convection boundary layer between it and the conductor ) in the box is $T_2$.

Its more accounting.

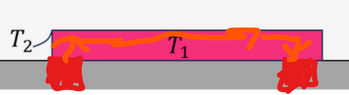
It's about the boundary area. Imagine it is a thin film, heat is transferred across it, and in the direction of flow. We ignore this last part, that's why $h$ changes along the length. We are hand waiving that away. As for the open duct, the flow entering/exiting does not have a convection boundary with itself...it requires relative motion.

As for the green area, whatever you want to do with it. In the case of a solid conductor the flow which carries heat away would hit it...relative motion. BUT its a pretty tiny area, its most likely not worth the trouble of factoring it in unless you want to keep options open for geometry changes.

Note: You may have to scroll to the right to see the full post.

Thanks! I think it's getting a bit to complicated, with to many unknown variables, it will not be possible to calculate a current. I will try to represent this problem statement, with a current that can actually be found, along with simplifications, and why they can be made. If any of the simplifications are not required, please let me know.

Problem Statement
Evaluate the ampacity of an uninsulated nickel strip that is 0.1 mm thick $t_{S}$, 10 mm wide $W$, and 63 mm long $L$. Additional details are intentionally not provided. This in alignment with current ratings of commercial cables that do not specify ambient air conditions, if the cable is within a container, or if additional insulation is placed around the cable. The orientation of the nickel strip is also not specified. Assume that it can be used in any orientation in outdoor conditions.

Assessment of ambient air conditions
We will take the liberty of assuming that the conductor will not be used in ambient temperature $T_{\infty}$ conditions greater than $100\;deg\;F$. This is a reasonable maximum temperature for most areas on the planet. There are certainly places that do not get this hot or places that get even hotter. However, because the current is dependent on the difference between the temperature of the strip $T_{S}$ and $T_{\infty}$, for safety reasons it is best to assume that $T_{\infty}$ is as large as possible for a variety of areas.
$$T_{\infty} = (100\;deg\;F - 32)\frac{5}{9} = 37\;\frac{7}{9}\;deg\;C$$
$$(37\;\frac{7}{9}\;deg\;C+273.15)\frac{K}{C}\;is\;about\;310.928\;K$$

Assessment of temperature of the strip
Nickel strips are typically used in the assembly of battery packs. Most cells have a maximum operating temperature of $T_{S} = 60\;deg\;C$. While this puts us at the absolute maximum temperature, it will become clear later on in this problem that the actual current we find is an underestimate, so being right at the boundary condition is acceptable.
$$(60\;deg\;C+273.15)\frac{K}{C} = 333.15\;K$$

$$\dot{Q} = Q_{1} + Q_{2} + Q_{3}...$$
Where:
$\dot{Q}$ is the total heat transferred.
$Q_{n}$ is a the nth heat transfer.

$$P = I_{A}^{2}\;R$$
Where:
$P$ is the power created by sending current through the strip.
$I_{A}^{2}$ is the ampacity current.
$R$ is the resistance of the strip.

$$R = \frac{\rho\;L}{A} = \frac{\rho\;L}{Wt_{S}}$$
Where:
$\rho$ is the resistivity of the material, for nickel it's $6.99 * 10^{-8} \Omega\;m$
$L$ is the length of the strip, parallel to the flow of current
$A$ is the surface area perpendicular to the flow of current
$W$ W is the width of the strip, perpendicular to the flow of current
$t_{S}$ is the thickness of the strip, perpendicular to the flow of current

$$P = I_{A}^{2}\;R = I_{A}^{2}\;\frac{\rho\;L}{Wt_{S}}$$
$$I_{A}^{2}\;\frac{\rho\;L}{Wt_{S}} = Q_{1} + Q_{2} + Q_{3}...$$
$$I_{A}^{2} = \frac{Wt_{S}}{\rho\;L}(Q_{1} + Q_{2} + Q_{3}...)$$
$$I_{A} = \sqrt{\frac{Wt_{S}}{\rho\;L}(Q_{1} + Q_{2} + Q_{3}...)}$$

Kapton Tape Insulation Thermal Specifications:
Thermal conductivity $k = 0.12 \frac{W}{m\;K}$.
Thickness $t_{I} = 0.03 mm$

Lithium Ion Cell Thermal Specifications:
Thermal conductivity $k = Unknown$
Thickness of 21700 cell $t = 70 mm$
Thickness of 18650 cell $t = 65 mm$

Heat Transfer via Convection:
$$Q =(T_{S} - T_{\infty})\sum_{n = 1}^{n} h_n*A_n$$
Where:
$h_{n}$ is the heat transfer coefficient of nth surface area.
$A_{n}$ is the nth surface area.
$T_{1}$ is the temperature of the hotter object
$T_{2}$ is the temperature of the colder object

Heat Transfer via Conduction
$$Q = \frac{kA(T_{1} - T_{2})}{t}$$
Where:
$t$ is the thickness of the material that heat is being transferred to.

There are many heat transfers that take place, and many temperatures that are unknown and cannot be calculated based on the six known variables $L\;W\;t\;T_{\infty}\;T_{S}\;\rho$
$$\sqrt{\frac{Wt}{\rho\;L}(Q_{1} + Q_{2} + Q_{3}...)} > \sqrt{\frac{Wt}{\rho\;L}Q_{1}}$$
Hence if we consider only convection of the strip in ambient temperature conditions T_{\infty}, it will produce a current value smaller than the actual value if we were to consider:

1. Heat transfer via conduction from the temperature difference between the cells and the strip
2. Heat transfer via conduction from the strip to the insulation from the temperature difference between the strip and the insulation
3. Heat transfer via radiation from the temperature difference between the insulation and other electrical components within the box
4. Heat transfer via convection from the temperature difference between the insulation and the air within the box
5. Heat transfer via convection from the temperature difference between the air in the box and the air outside of the box
6. Likely others that I'm forgetting...

We will consider the temperature of the cells, the temperature of the insulation, the temperature of the air within the box, all to be the same temperature as the strip. Hence, we will consider heat transfer via convection from the strip and the ambient air conditions.

Assessment of Surface Areas Exposed to Ambient Air Conditions
In order to provide the best estimation of the current, we will assume that the "bottom" of the strip is resting on some other surface, but we will not consider the heat transfer via conduction from the strip and this other material. Meaning that the strip is not "floating". Additionally we will assume that the other five surfaces of the strip are exposed to ambient air conditions. This is a reasonable assessment to make, considering that nickel strips are typically spot welded to cells (the thing that the strip is resting on). We will also assume that each surface area is at the same temperature. Meaning that each surface area is at $T_{S}$.

$$\dot{Q} =(T_{S} - T_{\infty})\sum_{n=1}^{5} h_n*A_n$$
$$A = LW + Wt + Wt + Lt + Lt = LW + 2Wt + 2Lt$$
$$\dot{Q} =(T_{S} - T_{\infty})(h_{LW}LW + 2h_{Wt}Wt + 2h_{Lt}Lt)$$
$$I_{A} = \sqrt{\frac{Wt}{\rho\;L}(T_{S} - T_{\infty})(h_{LW}LW + 2h_{Wt}Wt + 2h_{Lt}Lt)}$$



$$h_{n_{HV}} = \frac{k N_{n_{HV}}}{L_{C_{n_{HV}}}}$$
Where:
$h_{n_{HV}}$ is the heat transfer coefficient of surface area $n$ in either the horizontal $H$, Vertical $V$ orientation
$N_{n_{HV}}$ is Nusselt Number surface area $n$ in either the horizontal $H$, Vertical $V$ orientation
$L_{C_{n_{HV}}}$ is the characteristic length of surface area $n$ in either the horizontal $H$, Vertical $V$ orientation

$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{\frac{N_{LW_{HV}}}{L_{C_{LW_{HV}}}}LW + 2\frac{N_{Wt_{HV}}}{L_{C_{Wt_{HV}}}}Wt + 2\frac{N_{Lt_{HV}}}{L_{C_{Lt_{HV}}}}Lt}$$

There are three possible orientations that must be considered

Option	LW	Wt	Lt
1​	H	V	V
2​	V	H	V
3​	V	V	H

Characteristic Lengths
For Horizontal surfaces, it's the surface area divided by the perimeter
For Vertical or Inclined surfaces, it's the vertical height
$$L_{C_{LW_{H}}} = \frac{LW}{2L+2W}$$
$$L_{C_{LW_{V}}} = L\;or\;W$$
$$L_{C_{Wt_{H}}} = \frac{Wt}{2W+2t}$$
$$L_{C_{Wt_{V}}} = W\;or\;t$$
$$L_{C_{Lt_{H}}} = \frac{Lt}{2L+2t}$$
$$L_{C_{Lt_{V}}} = L\;or\;t$$

Option	LW	Wt	Lt
1​	H, L_C = LW/(2(L+W))	V, L_C = t	V, L_C = t
2​	V, L_C = L	H, L_C = Wt/(2(W+t))	V, L_C = L
3​	V, L_C = W	V, L_C = t	H, L_C = Lt/(2(L+t))

$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{\frac{N_{LW_{HV}}}{L_{C_{LW_{HV}}}}LW + 2\frac{N_{Wt_{HV}}}{L_{C_{Wt_{HV}}}}Wt + 2\frac{N_{Lt_{HV}}}{L_{C_{Lt_{HV}}}}Lt}$$
Option 1
$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{\frac{N_{LW_{H}}}{L_{C_{LW_{H}}}}LW + 2\frac{?_{Wt_{V}}}{L_{C_{Wt_{V}}}}Wt + 2\frac{?_{Lt_{V}}}{L_{C_{Lt_{V}}}}Lt}$$
$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{\frac{N_{LW_{H}}}{\frac{LW}{2(L+W)}}LW + 2\frac{N_{Wt_{V}}}{t}Wt + 2\frac{?_{Lt_{V}}}{t}Lt}$$
$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{2(L+W)N_{LW_{H}} + 2WN_{Wt_{V}}+ 2L?_{Lt_{V}}}$$
$$I_{A} = \sqrt{\frac{2kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{(L+W)N_{LW_{H}} + WN_{Wt_{V}}+ LN_{Lt_{V}}}$$
Option 2
$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{\frac{N_{LW_{V}}}{L_{C_{LW_{V}}}}LW + 2\frac{N_{Wt_{H}}}{L_{C_{Wt_{H}}}}Wt + 2\frac{N_{Lt_{V}}}{L_{C_{Lt_{V}}}}Lt}$$
$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{\frac{N_{LW_{V}}}{L}LW + 2\frac{N_{Wt_{H}}}{\frac{Wt}{2(W+t)}}Wt + 2\frac{N_{Lt_{V}}}{L}Lt}$$
$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{WN_{LW_{V}} + 2*2(W+t)N_{Wt_{H}} + 2tN_{Lt_{V}}}$$
$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{WN_{LW_{V}} + 4(W+t)?_{Wt_{H}} + 2tN_{Lt_{V}}}$$
Option 3
$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{\frac{N_{LW_{V}}}{L_{C_{LW_{V}}}}LW + 2\frac{N_{Wt_{V}}}{L_{C_{Wt_{V}}}}Wt + 2\frac{N_{Lt_{H}}}{L_{C_{Lt_{H}}}}Lt}$$
$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{\frac{N_{LW_{V}}}{W}LW + 2\frac{N_{Wt_{V}}}{t}Wt + 2\frac{N_{Lt_{H}}}{\frac{Lt}{2(L+t)}}Lt}$$
$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{LN_{LW_{V}} + 2WN_{Wt_{V}} + 2*2(L+t)N_{Lt_{H}}}$$
$$I_{A} = \sqrt{\frac{kWt}{\rho\;L}} \sqrt{T_{S} - T_{\infty}} \sqrt{LN_{LW_{V}} + 2WN_{Wt_{V}} + 4(L+t)N_{Lt_{H}}}$$

Rayleigh number
$$Ra_{L_{C}} = \frac{g\beta (T_{S} - T_{\infty})L_{C}^{3}}{v \alpha}$$
Where:
$Ra_{L_{C}}$ is the Rayleigh number of characteristic length $L_{C}$
$g$ is the acceleration due to gravity, $9.81456 \frac{m}{s^{2}}$.
$\beta$ is the expansion coefficient in $\frac{1}{K}$, $\beta = \frac{1}{T_{\infty}} = \frac{1}{333.15}\;\frac{1}{K}$
$v$ is the kinematic viscosity in $\frac{m^{2}}{s}$, $v =(-0.000000000000022928 \frac{m^{2}}{s\;K^{3}})T_{\infty}^{3} + (0.00000000011574 \frac{m^{2}}{s\;K^{2}})T_{\infty}^2 + (0.000000028239 \frac{m^{2}}{s\;K})T_{\infty} - (0.0000024125 \frac{m^{2}}{s}) =(-0.000000000000022928 \frac{m^{2}}{s\;K^{3}})*(310.928\;K)^{3} + (0.00000000011574 \frac{m^{2}}{s\;K^{2}})*(310.928\;K)^2 + (0.000000028239 \frac{m^{2}}{s\;K})*(310.928\;K) - (0.0000024125 \frac{m^{2}}{s})\;is\;about\;1.68679*10^{-5} \frac{m^{2}}{s}$
$\alpha$ is the thermal diffusivity in $\frac{m^{2}}{s}$, $\alpha = (-0.000000000000052324)T_{\infty}^{3} + (0.00000000018976)T_{\infty}^{2} + (0.0000000339)T_{\infty} - (0.000003888) = (-0.000000000000052324)(310.928\;K)^{3} + (0.00000000018976)(310.928\;K)^{2} + (0.0000000339)(310.928\;K) - (0.000003888)\;is\;about\;2.34249*10^{-5} \frac{m^{2}}{s}$
$$Ra_{L_{C}} = \frac{(9.81456 \frac{m}{s^{2}})(\frac{1}{333.15}\;\frac{1}{K}) (333.15 K - 310.928 K)}{(1.68679*10^{-5} \frac{m^{2}}{s}) (2.34249*10^{-5} \frac{m^{2}}{s})} L_{C}^{3} = (1.65682*10^{9} \frac{1}{m^{3}})L_{C}^{3}$$
Characteristic Lengths
$$t = 0.1 mm = (0.1 mm)(\frac{1}{10^{3}} \frac{m}{mm}) = 0.0001 m$$
$$W = 10 mm = (10 mm)(\frac{1}{10^{3}} \frac{m}{mm}) = 0.01 m$$
$$L = 63 mm = (63 mm)(\frac{1}{10^{3}} \frac{m}{mm}) = 0.063 m$$
$$\frac{LW}{2(L+W)} = \frac{0.063 m * 0.01 m}{2(0.063 m + 0.01 m)} = 0.07875 m$$
$$\frac{Wt}{2(W+t)} = \frac{0.01 m * 0.0001 m}{2(0.01 m + 0.0001 m)}\;is\;about\;0.0000495 m$$
$$\frac{Lt}{2(L+t)} = \frac{0.063 m * 0.0001 m}{2(0.063 m + 0.0001 m)}\;is\;about\;0.0000499 m$$
Rayleigh number Calculations
$$Ra_{\frac{LW}{2(L+W)}} = (1.65682*10^{9} \frac{1}{m^{3}})(0.07875 m)^{3}\;is\;about\;809146.232$$
$$Ra_{t} = (1.65682*10^{9} \frac{1}{m^{3}})(0.0001 m)^{3}\;is\;about\;0.00166$$
$$Ra_{L} = (1.65682*10^{9} \frac{1}{m^{3}})(0.063 m)^{3}\;is\;about\;414282.871$$
$$Ra_{\frac{Wt}{2(W+t)}} = (1.65682*10^{9} \frac{1}{m^{3}})(0.0000495 m)^{3}\;is\;about\;0.000201$$
$$Ra_{W} = (1.65682*10^{9} \frac{1}{m^{3}})(0.01 m)^{3} = 1656.82$$
$$Ra_{\frac{Lt}{2(L+t)}} = (1.65682*10^{9} \frac{1}{m^{3}})(0.0000499 m)^{3} = 0.000206$$

Option	LW	Wt	Lt
1​	H, L_C = LW/(2(L+W)), Ra ~ 809146.232	V, L_C = t, Ra = 0.00166	V, L_C = t, Ra = 0.00166
2​	V, L_C = L, Ra ~ 414282.871	H, L_C = Wt/(2(W+t)), Ra ~ 0.000201	V, L_C = L, Ra ~ 414282.871
3​	V, L_C = W, Ra = 1656.82	V, L_C = t, Ra = 0.00166	H, L_C = Lt/(2(L+t)), Ra ~ 0.000206

Prandt Number
$$Pr = \frac{c_{p}\;\mu}{k}$$
Where:
$Pr$ is Prandt Number
$c_{p}$ is the specific heat in $\frac{J}{kg K}$, $c_{p}\;is\;about\;1006.771\;\frac{J}{kg K}$
$\mu$ is the dynamic viscosity in $\frac{Kg}{m\;s}$, $\mu\;is\;about\;1.901*10^{-5}\;\frac{Kg}{m\;s}$
$k$ is the thermal conductivity in $\frac{W}{m\;K}$, $k\;is\;about\;0.026\;\frac{W}{m\;K}$
$$Pr = \frac{c_{p}\;\mu}{k} = \frac{1006.771*1.901*10^{-5}}{0.026}\;is\;about\;0.724

Nusselt Number
For horizontal plates:
$N = 0.54Ra^{1/4}$ for $10^5 < Ra < 2*10^{7}$
For turbulent flow:
$N = 0.14Ra^{1/3}$ for $10^5 < Ra < 2*10^{7}$
For vertical plates:
$$N = 0.68 + \frac{0.670*Ra^{1/4}}{(1+(\frac{0.492}{Pr})^{\frac{9}{16}})^{\frac{4}{9}}}$$
$$N = 0.68 + \frac{0.670*Ra^{1/4}}{(1+(\frac{0.492}{0.724})^{\frac{9}{16}})^{\frac{4}{9}}}$$
So:
$$N_{LW/(2(L+W))} = 0.54(809146.232)^{1/4} = 16.1957$$
$$N_{LW_{t}} = 0.68 + \frac{0.670*(0.00166)^{1/4}}{(1+(\frac{0.492}{0.724})^{\frac{9}{16}})^{\frac{4}{9}}}\;is\;about\;0.784$$
$$N_{L} = 0.68 + \frac{0.670*(414282.871)^{1/4}}{(1+(\frac{0.492}{0.724})^{\frac{9}{16}})^{\frac{4}{9}}}\;is\;about\;13.755$$
$$N_{Wt/(2(W+t))} =$$ Not Defined, Ra to small
$$N_{W} = 0.68 + \frac{0.670*(1656.82)^{1/4}}{(1+(\frac{0.492}{0.724})^{\frac{9}{16}})^{\frac{4}{9}}}\;is\;about\;3.96804$$
$$N_{Lt/(2(L+t))} =$$ Not Defined, Ra to small

Option	LW	Wt	Lt
1​	H, L_C = LW/(2(L+W)), Ra ~ 809146.232, N = 16.1957	V, L_C = t, Ra = 0.00166 N ~0.784	V, L_C = t, Ra = 0.00166 N ~0.784
2​	V, L_C = L, Ra ~ 414282.871 N ~ 13.755	H, L_C = Wt/(2(W+t)), Ra ~ 0.000201 N = Not Defined, Ra to small	V, L_C = L, Ra ~ 414282.871, N ~ 13.755
3​	V, L_C = W, Ra = 1656.82, N ~ 3.96804	V, L_C = t, Ra = 0.00166 N ~0.784	H, L_C = Lt/(2(L+t)), Ra ~ 0.000206 N = Not Defined, Ra to small

Option 1
$$I_{A} = \sqrt{\frac{2(0.026)(0.01)(0.0001)}{(6.99 * 10^{-8})(0.063)}} \sqrt{333.15 - 310.928} \sqrt{(0.063+0.01)(16.1957) + (0.01)(0.784)+ (0.063)(0.784)}\;is\;about\;18.0348 A$$

So does this look correct?
The current I got of over 18 A seems a bit high to me.
My values for Nusselt Number for orientation 2 and 3 are not defined because Rayleigh number is to small. I'm wondering if my values for
$v$ the kinematic viscosity of about $1.68679*10^{-5} \frac{m^{2}}{s}$ and $\alpha$ of about $2.34249*10^{-5} \frac{m^{2}}{s}$ are correct? They look ok to me.

Note the 18 A I got for the answer, is just what the numbers gave me, likely a mistake somewhere in my calculations, or assumptions I made, but I cannot find it. Theoretical exercise only to understand the calculations and concepts. I suspect it is WAY to high. I am NOT suggesting someone actually send this much current through a strip of these dimensions.

Thanks for any help!

 

[erobz]

View attachment 356660
There are many heat transfers that take place, and many temperatures that are unknown and cannot be calculated based on the six known variables $L\;W\;t\;T_{\infty}\;T_{S}\;\rho$

This is not correct. I think you are missing the forest from the trees. You must try to work with the overall process to understand what is going on. While the final transfer of power is that of convection, you can't just reduce it to that step to get the ss temp.
Thought Question( conceptual): If you have two boxes of exterior dimension $a,b,c,$. Inside each is an identical conductor generating $I^2 R$. One box is made of thin conductive material, like 1mm steel plate( high thermal conductivity). The other is constructed of 18 cm thick plastic( low thermal conductivity). Both at a steady state, which has the conductor of greater temperature inside it?

 

[BuddyBoy]

This is not correct. I think you are missing the forest from the trees. You must try to work with the overall process to understand what is going on. While the final transfer of power is that of convection, you can't just reduce it to that step to get the ss temp.
Thought Question( conceptual): If you have two boxes of exterior dimension $a,b,c,$. Inside each is an identical conductor generating $I^2 R$. One box is made of thin conductive material, like 1mm steel plate( high thermal conductivity). The other is constructed of 18 cm thick plastic( low thermal conductivity). Both at a steady state, which has the conductor of greater temperature inside it?

Thanks for the response and help!

I would say that the thick plastic box with low thermal conductivity would contain the higher temperature strip. This would be because convection wouldn't cool off the box as well, and heat would be more retained in the lower thermal conductivity.

So when I find $\dot{Q}$ for the nickel stirp, do I consider all heat transfer of the nickel strip and consider this to be one equation. Then find $\dot{Q}$ from the perspective of insulation as a second equation. Then find $\dot{Q}$ from the perspective of the battery box. Do I consider all heat transfers to be positive instead of negative? I'm thinking of something like this, from an electrical circuit perspective:

The heat transferred via convection from the cell to the strip is equal to heat transferred from the strip to the insulation. The whole thing of if you assume that current entering the node is positive, then current leaving the node is negative. The two are equal to each other
$$Q_{Conduction\;Cells\;to\;Strip} = Q_{Conduction\;Strip\;to\;Insulation}$$

Equation 1:
$$Q_{Conduction\;Cells\;to\;Strip} = Q_{Conduction\;Strip\;to\;Insulation} = I^{2}R$$
$Q_{Conduction\;Cells\;to\;Strip}$ will likely not be able to determine. But I suppose if my assumption is correct, $Q_{Conduction\;Strip\;to\;Insulation}$ can be calculated, therefore I would know $Q_{Conduction\;Cells\;to\;Strip}$.

Equation 2:
$$Q_{Conduction\;Strip\;to\;Insulation} = Q_{Convection\;Insulation\;to\;Air\;in\;Box}$$

Equation 3:
$$Q_{Convection\;Air\;in\;Box\;to\;Box} = Q_{Convection\;Box\;to\;Ambient\;Air}$$

Now showing each transfer as a function of the temperatures:
$$Q_{Conduction\;Strip\;to\;Insulation}(T_{Strip}, T_{Insulation\;1})$$
$$Q_{Convection\;Insulation\;to\;Air\;in\;Box}(T_{Insulation\;2}, T_{Air\;in\;Box})$$
$$Q_{Convection\;Air\;in\;Box\;to\;Box}(T_{Air\;in\;Box}, T_{Box\;1})$$
$$Q_{Convection\;Box\;to\;Ambient\;Air}(T_{Box\;2}, T_{infty})$$

Where the first temperature is hotter than the second temperature. Meaning $T_{Box\;1} > T_{Box\;2}$

How to solve the problem:

1. $$Q_{Conduction\;Strip\;to\;Insulation} = I^{2}R$$. Solve the equation for $T_{Strip} - T_{Insulation\;1}$ as a function of current. Lets call this function F1
2. Solve $$Q_{Conduction\;Strip\;to\;Insulation} = Q_{Convection\;Insulation\;to\;Air\;in\;Box}$$ for $T_{Insulation\;2} - T_{Air\;in\;Box}$ as a function of $T_{Strip} - T_{Insulation\;1}$. Lets call this function F2
3. Solve $$Q_{Convection\;Air\;in\;Box\;to\;Box} = Q_{Convection\;Box\;to\;Ambient\;Air}$$ for $T_{Box\;2} - T_{\infty}$ as a function of $T_{Insulation\;2} - T_{Air\;in\;Box}$. Lets call this function F3
4. Insert function F2 into function F3. Now I have a function for $T_{Box\;2} - T_{\infty}$ as a function of $T_{Strip} - T_{Insulation\;1}$. Lets call this function F4
5. Insert Function F1 into function F4. Now I have a function for $T_{Box\;2} - T_{\infty}$ as a function of current. Lets call this function F5.

I think I'm getting closer in trying to understand how to solve this problem. But I would still have an unknown variable of the temperature of the outside of the battery box. I'm not seeing a way to solve for it.

I really do appreciate the help here with this! I'm wondering if I'm on the right track? Even if I disregarding the insulation, I would still have an issue of not knowing the temperature of the outside of the box, and I'm not seeing a way to find it.

 

[erobz]

Thanks for the response and help!

I would say that the thick plastic box with low thermal conductivity would contain the higher temperature strip. This would be because convection wouldn't cool off the box as well, and heat would be more retained in the lower thermal conductivity.

So when I find $\dot{Q}$ for the nickel stirp, do I consider all heat transfer of the nickel strip and consider this to be one equation. Then find $\dot{Q}$ from the perspective of insulation as a second equation. Then find $\dot{Q}$ from the perspective of the battery box. Do I consider all heat transfers to be positive instead of negative? I'm thinking of something like this, from an electrical circuit perspective:
View attachment 356692
The heat transferred via convection from the cell to the strip is equal to heat transferred from the strip to the insulation. The whole thing of if you assume that current entering the node is positive, then current leaving the node is negative. The two are equal to each other
$$Q_{Conduction\;Cells\;to\;Strip} = Q_{Conduction\;Strip\;to\;Insulation}$$

Equation 1:
$$Q_{Conduction\;Cells\;to\;Strip} = Q_{Conduction\;Strip\;to\;Insulation} = I^{2}R$$
$Q_{Conduction\;Cells\;to\;Strip}$ will likely not be able to determine. But I suppose if my assumption is correct, $Q_{Conduction\;Strip\;to\;Insulation}$ can be calculated, therefore I would know $Q_{Conduction\;Cells\;to\;Strip}$.

Equation 2:
$$Q_{Conduction\;Strip\;to\;Insulation} = Q_{Convection\;Insulation\;to\;Air\;in\;Box}$$

Equation 3:
$$Q_{Convection\;Air\;in\;Box\;to\;Box} = Q_{Convection\;Box\;to\;Ambient\;Air}$$

Now showing each transfer as a function of the temperatures:
$$Q_{Conduction\;Strip\;to\;Insulation}(T_{Strip}, T_{Insulation\;1})$$
$$Q_{Convection\;Insulation\;to\;Air\;in\;Box}(T_{Insulation\;2}, T_{Air\;in\;Box})$$
$$Q_{Convection\;Air\;in\;Box\;to\;Box}(T_{Air\;in\;Box}, T_{Box\;1})$$
$$Q_{Convection\;Box\;to\;Ambient\;Air}(T_{Box\;2}, T_{infty})$$

Where the first temperature is hotter than the second temperature. Meaning $T_{Box\;1} > T_{Box\;2}$

How to solve the problem:

1. $$Q_{Conduction\;Strip\;to\;Insulation} = I^{2}R$$. Solve the equation for $T_{Strip} - T_{Insulation\;1}$ as a function of current. Lets call this function F1
2. Solve $$Q_{Conduction\;Strip\;to\;Insulation} = Q_{Convection\;Insulation\;to\;Air\;in\;Box}$$ for $T_{Insulation\;2} - T_{Air\;in\;Box}$ as a function of $T_{Strip} - T_{Insulation\;1}$. Lets call this function F2
3. Solve $$Q_{Convection\;Air\;in\;Box\;to\;Box} = Q_{Convection\;Box\;to\;Ambient\;Air}$$ for $T_{Box\;2} - T_{\infty}$ as a function of $T_{Insulation\;2} - T_{Air\;in\;Box}$. Lets call this function F3
4. Insert function F2 into function F3. Now I have a function for $T_{Box\;2} - T_{\infty}$ as a function of $T_{Strip} - T_{Insulation\;1}$. Lets call this function F4
5. Insert Function F1 into function F4. Now I have a function for $T_{Box\;2} - T_{\infty}$ as a function of current. Lets call this function F5.

I think I'm getting closer in trying to understand how to solve this problem. But I would still have an unknown variable of the temperature of the outside of the battery box. I'm not seeing a way to solve for it.

I really do appreciate the help here with this! I'm wondering if I'm on the right track? Even if I disregarding the insulation, I would still have an issue of not knowing the temperature of the outside of the box, and I'm not seeing a way to find it.

It’s late here, but here is something to chew on. You will apply surface energy balances working your way out or in. When you get to a wall/air boundary apply:

$$-k\left. \frac{dT}{dx}\right|_{x=0}= h(T-T_{\infty})$$

Then apply conduction to get through the wall to the next boundary temp,( x=0 just means evaluate the derivative at the boundary in question). Then to get across the convection boundary on that side re apply the equation above. I haven’t gone through this fully but I can’t see why we shouldn’t be able to find a solution for this.

P.S. correct, the conductor in the thick plastic box will have higher SS temp, all other things the same.

 

[BuddyBoy]

It’s late here, but here is something to chew on. You will apply surface energy balances working your way out or in. When you get to a wall/air boundary apply:

$$-k\left. \frac{dT}{dx}\right|_{x=0}= h(T-T_{\infty})$$

Then apply conduction to get through the wall to the next boundary temp,( x=0 just means evaluate the derivative at the boundary in question). Then to get across the convection boundary on that side re apply the equation above. I haven’t gone through this fully but I can’t see why we shouldn’t be able to find a solution for this.

P.S. correct, the conductor in the thick plastic box will have higher SS temp, all other things the same.

Note you may have to scroll to the right to see the full equations.

I see. Thanks for pointing this out! so I think it's something like this give, this guidance.

Using the image above, and ignoring any insulation, conduction from the bottom of the strip to the box.

Power generated in conductor equals heat transferred via natural of the strip to air within the box:
$$I_{A}^{2}R = (T_{1} - T{2})\sum_{n_{S} = 1}^{5} h_{n_{S}} * A_{n_{s}}$$
Solving for $T_{1} - T{2}$
$$T_{1} - T_{2} = \frac{I_{A}^{2}R}{\sum_{n_{S} = 1}^{5} h_{n_{S}} * A_{n_{s}}}$$

Heat transferred via natural convection from the air in the box to the strip equals heat transferred from the air in the box, to the inner surface of the box via natural convection
$$(T_{1} - T_{2})\sum_{n_{S} = 1}^{5} h_{n_{S}} * A_{n_{s}} = (T_{2} - T_{3})\sum_{n_{B1} = 1}^{5} h_{n_{B1}} * A_{n_{B1}}$$
Plugging in the first equation into the equation above
$$I_{A}^{2}R = (T_{2} - T_{3})\sum_{n_{B1} = 1}^{5} h_{n_{B1}} * A_{n_{B1}}$$
Solving for $T_{2} - T{3}$
$$T_{2} - T_{3} = \frac{I_{A}^{2}R}{\sum_{n_{B1} = 1}^{5} h_{n_{B1}} * A_{n_{B1}}}$$

Heat transferred via natural convection from the air in the box to the inner surface of the box via natural convection equals the heat transferred via conduction from the inner surface of the box to the outer surface of the box
$$(T_{2} - T_{3})\sum_{n_{B} = 1}^{5} h_{n_{B}} * A_{n_{B}} = (T_{3} - T_{4})\frac{k_{B}}{t_{B}}\sum_{n_{B2} = 1}^{5} A_{n_{B2}}$$
Plugging in the first equation to the equation above
$$I_{A}^{2}R = (T_{3} - T_{4})\frac{k_{B}}{t_{B}}\sum_{n_{B2} = 1}^{5} A_{n_{B2}}$$
Solving for $T_{3} - T{4}$
$$T_{3} - T{4} = \frac{I_{A}^{2}R}{\frac{k_{B}}{t_{B}}\sum_{n_{B2} = 1}^{5} A_{n_{B2}}}$$

Heat transfer via conduction from the inner surface of the box to the outer surface of the box is equal to the heat transferred from the outer surface of the box to ambient temperature via natural convection
$$(T_{3} - T_{4})\frac{k_{B}}{t_{B}}\sum_{n_{B2} = 1}^{5} A_{n_{B2}} = (T_{4} - T_{\infty})\sum_{n_{B3} = 1}^{5} h_{n_{B3}} * A_{n_{B3}}$$
Plugging in the first equation to the equation above
$$I_{A}^{2}R = (T_{4} - T_{\infty})\sum_{n_{B3} = 1}^{5} h_{n_{B3}} * A_{n_{B3}}$$
Solving for $T_{4} - T_{\infty}$
$$T_{4} - T_{\infty} = \frac{I_{A}^{2}R}{\sum_{n_{B3} = 1}^{5} h_{n_{B3}} * A_{n_{B3}}}$$

Now
$$(T_{1} - T_{2}) + (T_{2} - T_{3}) + (T_{3} - T_{4}) + (T_{4} - T_{\infty})$$
$$T_{1} - T_{2} + T_{2} - T_{3} + T_{3} - T_{4} + T_{4} - T_{\infty} = T_{1} - T_{\infty}$$
Setting the two equations above equal to each other:
$$T_{1} - T_{\infty} = (T_{1} - T_{2}) + (T_{2} - T_{3}) + (T_{3} - T_{4}) + (T_{4} - T_{\infty})$$
Using the equations found for the temperature differences:
$$T_{1} - T_{\infty} = \frac{I_{A}^{2}R}{\sum_{n_{S} = 1}^{5} h_{n_{S}} * A_{n_{s}}} + \frac{I_{A}^{2}R}{\sum_{n_{B1} = 1}^{5} h_{n_{B1}} * A_{n_{B1}}} + \frac{I_{A}^{2}R}{\frac{k_{B}}{t_{B}}\sum_{n_{B2} = 1}^{5} A_{n_{B2}}} + \frac{I_{A}^{2}R}{\sum_{n_{B3} = 1}^{5} h_{n_{B3}} * A_{n_{B3}}}$$
$$T_{1} - T_{\infty} = I_{A}^{2}R(\frac{1}{\sum_{n_{S} = 1}^{5} h_{n_{S}} * A_{n_{s}}} + \frac{1}{\sum_{n_{B1} = 1}^{5} h_{n_{B1}} * A_{n_{B1}}} + \frac{1}{\frac{k_{B}}{t_{B}}\sum_{n_{B2} = 1}^{5} A_{n_{B2}}} + \frac{1}{\sum_{n_{B3} = 1}^{5} h_{n_{B3}} * A_{n_{B3}}})$$
$$I_{A}^{2}R = \frac{T_{1} - T_{\infty}}{\frac{1}{\sum_{n_{S} = 1}^{5} h_{n_{S}} * A_{n_{s}}} + \frac{1}{\sum_{n_{B1} = 1}^{5} h_{n_{B1}} * A_{n_{B1}}} + \frac{1}{\frac{k_{B}}{t_{B}}\sum_{n_{B2} = 1}^{5} A_{n_{B2}}} + \frac{1}{\sum_{n_{B3} = 1}^{5} h_{n_{B3}} * A_{n_{B3}}}}$$
$$I_{A}^{2} = \frac{T_{1} - T_{\infty}}{R(\frac{1}{\sum_{n_{S} = 1}^{5} h_{n_{S}} * A_{n_{s}}} + \frac{1}{\sum_{n_{B1} = 1}^{5} h_{n_{B1}} * A_{n_{B1}}} + \frac{1}{\frac{k_{B}}{t_{B}}\sum_{n_{B2} = 1}^{5} A_{n_{B2}}} + \frac{1}{\sum_{n_{B3} = 1}^{5} h_{n_{B3}} * A_{n_{B3}}})}$$
$$I_{A} = \sqrt{\frac{T_{1} - T_{\infty}}{R(\frac{1}{\sum_{n_{S} = 1}^{5} h_{n_{S}} * A_{n_{s}}} + \frac{1}{\sum_{n_{B1} = 1}^{5} h_{n_{B1}} * A_{n_{B1}}} + \frac{1}{\frac{k_{B}}{t_{B}}\sum_{n_{B2} = 1}^{5} A_{n_{B2}}} + \frac{1}{\sum_{n_{B3} = 1}^{5} h_{n_{B3}} * A_{n_{B3}}})}}$$

And Bingo was his name? It looks like if I did this correctly, I would in theory have everything I would need to calculate the current of a strip of given dimensions, provided a desired surface temperature of the strip, the temperature of the ambient air, the thickness of the box, the inner and outer dimensions of the box, and the thermal conductivity of the box?

I really appreciate the help with this!

 

[erobz]

That all looks reasonable to me, good job!

 

[BuddyBoy]

That all looks reasonable to me, good job!

Thanks for your help through this process! Defiantly learned a lot through it. Seems like the generic equation is:

$$I = \sqrt{\frac{T_{1} - T_{\infty}}{R\sum_{}^{} R_{T}}}$$

Where R is the resistance of the strip, and RT is the thermal resistance.

Once conceptual question I have is shown in the example below:

Assume that the battery pack contains many nickel strips, connecting cells in series and parallel. The overall current used from the pack is $I_{A}$. All series connections experience the full $I_{A}$ current. Items in series experience the same current. If the series connections are made up of more than one piece of nickel strip, but of same width and thickness connections, perhaps of different length, $L_{1}$ and $L_{2}$, are in the same box discussed above. Each of the two strips see $I_{A}$.

Now as far as the total heat transferred into the air within the box, do I need to consider the total volume of "all" strips experiencing $I_{A}$, since each strip contributes to the overall heat transfer to air within the box, even though it's the same current $I_{A}$? Meaning do the presence of additional separate nickel strips experiencing the same current, impact the overall current that can be handled by each individual separate strip?

One additional conceptual question I have, I see that $h$ is dependent on the orientation. But how is this impacted for my strip for the heat transferred from the strip to the air in the box? So say for example while my battery box is at rest on a table, the strip is perfectly perpendicular to the table and is considered vertical. If I rotate the entire box (and therefore the strip as well) so that it is now horizontal, from my perspective outside of the box, the strip is now horizontal. However from the perspective relative to the air within the box, the strip is still vertical and hasn't changed orientation, and I should still consider it as vertical? Meaning vertical and horizontal is from relative to what perspective? Maybe I'm just confusing this and making it more complicated. Certainly if I rotate a strip in ambient air from vertical to horizontal, the strip is now horizontal. But if I'm not considering open ambient air in the atmosphere, but air within a container, and the whole container and therefore the air within it rotates with the strip, I have a slightly different situation, and I'm not sure if I need to take into consideration perspective?

 

[Tom.G]

Your image shows two strips of batteries, each strip has the batteries in parallel.

Now, if the batteries are supplying (or consuming) a current, the current in the strip will vary along its length because each battery is sharing the current load.

Cheers,
Tom

 

[BuddyBoy]

Your image shows two strips of batteries, each strip has the batteries in parallel.

Now, if the batteries are supplying (or consuming) a current, the current in the strip will vary along its length because each battery is sharing the current load.

Cheers,
Tom

Sorry for not showing this properly.

One one side you have something like this. On the other something like shown in the other figure. Theoretical thought exercise only here to understand concepts:

Assume that the copper bus bar in the second figure is nickel. This gives me a 5P2S pack.
The second image shows that $I_{A}$ would get divided up amongst the total surface area of all the strips connected the positive connections to the negative connections, creating the series and parallel connections.

I see your point here though. At BAT + and BAT - I'm seeing the full current, however as you go down the length of the strip, you would be seeing $I_{A}$ drop off assuming each cell contribute equally, $\frac{1}{5}$. I suppose you could vary the length, width and thickness somehow, maybe by "stacking" identical additional strips on top of each Strip 1 and Strip 2, to increase the thickness. I need to figure out how increasing the thickness impacts current carrying abilities.

My theoretical question I guess though is that does the presence of additional physically separate nickel strips within the box impact the current carrying capability of each individual strip?

Certainly if I take heat transfer via radiation into consideration, absolutely! But estimating this seems difficult. I don't know if I can negate radiation effects by insulating with Kapton tape? I guess even if I disregard radiation, does the presence of other strips impact the current carrying capability of other strips, due to more convection into the air within the box? Even though it's still the same maximum current going through the pack?

 

[pbuk]

I guess even if I disregard radiation, does the presence of other strips impact the current carrying capability of other strips, due to more convection into the air within the box? Even though it's still the same maximum current going through the pack?

Why are you asking this question? For mechanical reasons the strips that connect cells or batteries together are of such a size that their resistance is negligible in comparison with the internal resistance of the cells: battery packs heat up because of battery chemistry, not conductor resistivity.

 

[erobz]

Thanks for your help through this process! Defiantly learned a lot through it. Seems like the generic equation is:

$$I = \sqrt{\frac{T_{1} - T_{\infty}}{R\sum_{}^{} R_{T}}}$$

Where R is the resistance of the strip, and RT is the thermal resistance.

I wouldn't say that its a generic or general solution. We have implicitly made assumptions specific to the problem that are not generally true. For instance, if there was a wall that was thicker than another the inside temperature on that wall is different than the others (your solution assumes all interior wall at $T_3$ reasonable approximation perhaps - but I think none the less not general, or generic), different convection coefficients changes the temps ,having different wall temps (if significant) can introduce radiation...another complication. At best I think you have an outline for how might proceed to find a "more general" solution. The stuff you find in intro textbooks is "plane walls" for a reason. Fundamentally you are just going to have to work from principles. I just don't want you to start confidently overapplying it.

I was trying to help you get somewhere on it, but also don't want to try and translate a course on heat/mass transfer just so you can solve this(I think you have some very deep goals). Are you taking this course in college?

 

[BuddyBoy]

Thanks for the responses!

Why are you asking this question? For mechanical reasons the strips that connect cells or batteries together are of such a size that their resistance is negligible in comparison with the internal resistance of the cells: battery packs heat up because of battery chemistry, not conductor resistivity.

I'm asking this question, to attempt to apply a more practical application of the theoretical concepts learned from the oversimplified question asked, of how to theoretically calculate how much current can go through a strip of nickel strip in a battery pack in order to maintain a certain surface temperature.

Nickel strips are used in battery packs. Different thicknesses, widths, and lengths are available. But how do you know which dimensions to use if you wish your battery pack to output current $I$, if the rest of the battery pack is built properly (i.e., properly rated batteries and BMS).

I've learned good things so far from the oversimplified question originally asked, of just a nickel strip sitting in a box:

1. A common misconception (from the concepts and equations learned from this topic) is that length has no effect on the current carrying capability. This appears to be NOT true.
2. A common misconception is that doubling the width or thickness doubles the current carrying capability. This appears to be NOT true.
3. Even the orientation of the strip, seems to have an impact on the current carrying capability.

Certainly though, if you use a nickel strip to small in dimensions, yes it will carry the current, but it will get to hot, past the operating temperature ratings of the cells. If you want to stay under the operating temperature of the cells, how do you know what dimension of nickel to use?

Well thinking about this in greater detail here... If the cell is rated to output current $I$ under the operating temperature $T_{Cell}$. Then the cell can output $I$, no problem. However, if the nickel strip that it is connected to is not properly sized, the nickel stirp will heat up, possibly past $T_{Cell}$. Then conduction between the strip and the cell will occur, and the cell could heat up past $T_{Cell}$. So if I can figure out the size of the nickel strip at current $I$ at a temperature under $T_{Cell}$ (plus a safety margin), then there is no need to worry about the cell getting to $T_{Cell}$.

Any ideas?

I wouldn't say that its a generic or general solution. We have implicitly made assumptions specific to the problem that are not generally true. For instance, if there was a wall that was thicker than another the inside temperature on that wall is different than the others (your solution assumes all interior wall at $T_3$ reasonable approximation perhaps - but I think none the less not general, or generic), different convection coefficients changes the temps ,having different wall temps (if significant) can introduce radiation...another complication. At best I think you have an outline for how might proceed to find a "more general" solution. The stuff you find in intro textbooks is "plane walls" for a reason. Fundamentally you are just going to have to work from principles. I just don't want you to start confidently overapplying it.

I was trying to help you get somewhere on it, but also don't want to try and translate a course on heat/mass transfer just so you can solve this(I think you have some very deep goals). Are you taking this course in college?

Thanks for pointing the assumptions. They make sense. This isn't for a college course, just trying to understand a theoretical practical problem.

I'm thinking more and more that perhaps this problem cannot be solved, and experimental data is required? I suppose this is possible, but this seems like a very time consuming process. So I would like to at least think there's a way to calculate the dimensions given desired current.

 

[pbuk]

I'm asking this question, to attempt to apply a more practical application of the theoretical concepts learned from the oversimplified question asked, of how to theoretically calculate how much current can go through a strip of nickel strip in a battery pack in order to maintain a certain surface temperature.

In almost all practical applications, surface temperature is not a design limitation. Any nickel strip of sufficient dimensions to satisfy the mechanical requirements (mainly the connections to the individual cells) will have negligible resistivity. To understand this better, obtain some battery packs with nickel strip connections and measure them.

A common misconception (from the concepts and equations learned from this topic) is that length has no effect on the current carrying capability. This appears to be NOT true.

This is not a misconception. Your calculations depend on length because you are assuming heat dissipation from the ends of the conductor however in any application where ampacity is relevant the ends of the conductor are (i) connected to something so unable to dissipate heat; and (ii) negligible compared to the length of the conductor.

A common misconception is that doubling the width or thickness doubles the current carrying capability.

Do you have any evidence that this is a common misconception?

Even the orientation of the strip, seems to have an impact on the current carrying capability.

Yes, so when we are concerned with ampacity and convection is a significant factor in heat dissipation (e.g. in a "clipped direct" fixing as used in UK consumer wiring tables), vertical orientation is assumed. These tables are also based on a standard configuration of conductors (e.g. flat twin and earth) and insulation so cannot be derived by calculations on an isolated conductor in free air.

Certainly though, if you use a nickel strip to small in dimensions, yes it will carry the current, but it will get to hot, past the operating temperature ratings of the cells. If you want to stay under the operating temperature of the cells, how do you know what dimension of nickel to use?

Any dimension of nickel strip that you can fix mechanically to the cells will have negligible resistance.

 

[BuddyBoy]

In almost all practical applications, surface temperature is not a design limitation. Any nickel strip of sufficient dimensions to satisfy the mechanical requirements (mainly the connections to the individual cells) will have negligible resistivity. To understand this better, obtain some battery packs with nickel strip connections and measure them.


This is not a misconception. Your calculations depend on length because you are assuming heat dissipation from the ends of the conductor however in any application where ampacity is relevant the ends of the conductor are (i) connected to something so unable to dissipate heat; and (ii) negligible compared to the length of the conductor.


Do you have any evidence that this is a common misconception?


Yes, so when we are concerned with ampacity and convection is a significant factor in heat dissipation (e.g. in a "clipped direct" fixing as used in UK consumer wiring tables), vertical orientation is assumed. These tables are also based on a standard configuration of conductors (e.g. flat twin and earth) and insulation so cannot be derived by calculations on an isolated conductor in free air.


Any dimension of nickel strip that you can fix mechanically to the cells will have negligible resistance.

Hey thanks. I've seen that commercial power tool battery packs:

Appears to use at most 0.2 mm thick nickel, and very uncommon I have seen 0.3 mm thick. Appears to be about 10 mm wide or so. I'll also note that the majority of he nickel is in the "vertical" position with regards to the LW and Lt surface areas. If you rotate the battery pack horizontally, and the air within it, I'm not sure if the plates are still considered "vertical".

I'm not so sure I understand the concept that "any" dimension strip will work. Could you help me understand this a bit better? I think you might be right, but I'm struggling a bit to understand.

$$P = I^{2}R$$

So if $R$ is small so will be the "heat" generated, $P$ in terms of watts. However at some point as the current increases, I would imagine $P$ would be so large that the surface temperature of the nickel strip would get to hot, and it could eventually reach the maximum operating temperature of the cell? I'm not sure if there's a way to determine what this $P$ value is?

I see that if something else was connected to the Wt surface areas, than there is no conduction from that surface area. If you consider the Wt surface areas to be small, than the L term cancels out.

Sorry, just my thoughts that I think some people think "stacking" nickel helps much.

I wisht there was an ampacity table for nickel, given dimensions. However every table I see has different values! So I don't know which table to trust, or if it is experimentally obtained data only, and cannot be calculated?

I think calculating the temperature surface of a nickel strip "floating" in ambient area, given the dimensions, and ambient temperature, can be calculated. Could even calculate what would be if you insulate it.

At the very least we can say based on
$$I = \sqrt{\frac{T_{1} - T_{\infty}}{R*R_{T}}}$$
That the $R_{T}$ term is larger for when it is stored within a battery box, over ambient air. And because
$$I \alpha \frac{1}{\sqrt{R_{T}}}$$
So as $R_{T}$ gets larger $I$ gets smaller
So you can find the current given the dimensions, ambient temperature, desired surface temperature. Then you can say that the actual number for when it's in a battery box needs to be smaller than this. But by how much is unknown.

Some other values you would know when designing a battery pack:
Trying to think about other details here. You can measure the internal resistance of each cell. You can estimate how much nickel strip you are using and it's resistance. But you wouldn't know the resistance of the BMS. But you can also simply use a multimeter on the connector on the outside of the battery box enclosure and measure the internal resistance of the battery pack as a whole. Then the difference would give you resistance of the BMS.

So if you measure the internal resistance of the battery pack as whole from outside of the box, and you know the current you want to drain from it.

$$P = I^{2}R$$

You can know the total power consumed by the battery pack from it's internal resistance. But I'm not sure if this is useful.

 

[pbuk]

Hey thanks. I've seen that commercial power tool battery packs:
View attachment 356849
Appears to use at most 0.2 mm thick nickel, and very uncommon I have seen 0.3 mm thick. Appears to be about 10 mm wide or so.

So what is the cross-sectional area, in metres? Have you looked up the resistivity of nickel? If so, what is the resistance of, say, a strip 20cm long? What is the maximum current that you will draw from the battery pack? And what therefore will be the power that the strip needs to dissipate?

I'll also note that the majority of he nickel is in the "vertical" position with regards to the LW and Lt surface areas. If you rotate the battery pack horizontally, and the air within it, I'm not sure if the plates are still considered "vertical".

You have already been told that orientation of the strip is only relevant if heat loss by convection is significant. Do you think there is any convection inside the battery pack?

But you can also simply use a multimeter on the connector on the outside of the battery box enclosure and measure the internal resistance of the battery pack as a whole.

No, you cannot measure the internal resistance of a battery with a multimeter.

I think you should stop thinking about designing battery packs and learn some electronics.

 

[Steve4Physics]

You can know the total power consumed by the battery pack from it's internal resistance. But I'm not sure if this is useful.

Note that a battery's eletrolytes have electrical resistance - this is the main source of a battery's internal heating when current flows. Note that some of this heat will be thermally conducted to any nickel strips, making them hotter. This could be a larger effect than Ohmic heating from current passing through the strips.

The type of ampacity calculation you are considering does not take this into account.