How Do You Derive the Full Energy Momentum Relation Using Lorentz Factor?

[Glenn G]

Hi community,
There is a step on the wiki page about a derivation.

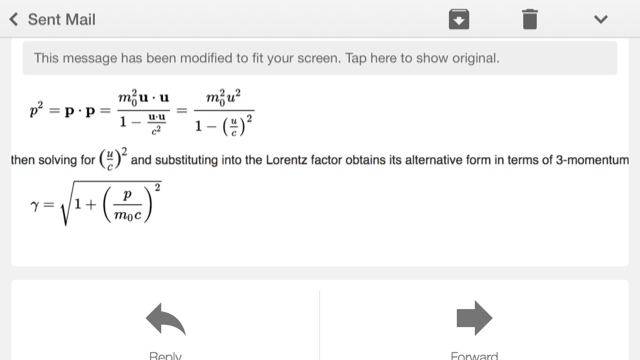
I don't seem to get the same thing when I try and solve for (u/c)^2 and then plug into Lorentz factor to get the new Lorentz factor so you can get the full energy momentum relation

My gamma term looks more like 1/ ((mo^2u^2/p^2))^-1/2 when I've subbed for (u/c)^2??

Can anyone help or any other resources to show easy as poss how to derive the full equation?
Thanks
G.

 

[Orodruin]

If you have a u left in your expression you have not solved for (u/c)^2 ...

 

[Glenn G]

I rearranged the top expression and made (u/c)^2 the subject but then you still have the u^2 that was in the numerator of the momentum expression? Confused.

 

[Orodruin]

Yes, so you have not solved for u^2/c^2. You need to actually solve for u^2/c^2.

Edit: Hint: Solve for u^2. The speed of light is just a constant.

 

[Glenn G]

I got this far and became a bit convoluted. Will try for u^2 then.
Thanks.
G.

 

[Orodruin]

Hint:
$$
1 = \frac{m^2 c^2 + p^2}{m^2 c^2 + p^2}
$$
...

 

[Glenn G]

Ooh, that's cheeky. I'll have another play this evening, thanks Orodruin.

 

[Glenn G]

Got it finally, quite satisfying ...