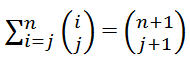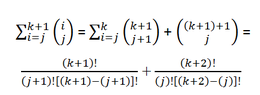wittysoup
- 7
- 0
Hello all,
I need a little help with how to go about proving the following:
View attachment 619
the formula for n choose k is n!/(k!(n-k)!)
For this, I have proceeded as follows:
Base case P(j):
View attachment 620
I am not sure if this is correct... but the next step would be to Assume P(k), I get stuck at that step because the algebraic expression does not look right... Am I going about this the right way? Thanks.
I need a little help with how to go about proving the following:
View attachment 619
the formula for n choose k is n!/(k!(n-k)!)
For this, I have proceeded as follows:
Base case P(j):
View attachment 620
I am not sure if this is correct... but the next step would be to Assume P(k), I get stuck at that step because the algebraic expression does not look right... Am I going about this the right way? Thanks.