How do you resolve seeming contradictions in SR?

[curiousburke]

Yes, I certainly didn't mean to suggest this problem I was having in thinking about two frames contracting was a contradiction as much as it was frying my brain.

 

[robphy]

On a spacetime diagram,
simultaneity is described using the Minkowski version of the "tangent-line to a circle".
More specifically, when one intersects a circle by a radial line,
the tangent-line at that intersection is orthogonal to the radial line...
in the geometry determined by the "circle".

Try it at:
robphy SIMULTANEITY spacetime diagrammer for relativity (simplified from v8c) - 2023
https://www.desmos.com/calculator/ajktes8bp5
Euclidean (E= -1), Minkowski/Special Relativity (E = +1), Galilean Relativity (E = 0)

 

[Ibix]

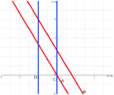
Here are a few spacetime diagrams. If you haven't come across them, they're simply plots of the position of an object over time, the custom being that time goes up the page. So a vertical line represents an object that isn't moving, and a line slanted to the left indicates one moving to the left. You may have come across these (usually with time horizontally) as "displacement-time graphs" in high school physics. We take them a little more seriously in relativity, since spacetime is a thing - these are maps of spacetime, and the lines are the 4d objects inhabiting it. You see one 3d slice at a time.

So here's your scenario, with my extra "D" observer. A and B are marked in red and are stationary, C and D are marked in blue and moving to the right.

Note that, in this frame, C and D are closer together than A and B - the horizontal distance between the lines ("the space between them") is shorter.

We could mark on the diagram the start and end of the experiment - when C passes A and then B. Let's do that with fine red lines:

Now comes the interesting part. C and D don't use the same definition of simultaneity. The lines in spacetime they call "now" are not horizontal lines on this diagram - they're sloped. In fact they are the fine blue lines on this graph:

Note that these lines still go through the A/C and B/C meetings. But if you look at the lower fine line, you can see it passes through B much later than the fine red line did. So according to C, at the start of the experiment B's clock was ahead. And the part of B's line that is "during the experiment" according to C (the part between the fine blue lines) is much shorter than the part that is "during the experiment" according to A and B - that is, it starts ahead and ticks slower.

This is also why length contraction doesn't lead to a contradiction. Length is measured at one time, and the frames have different definitions of "at one time". A and B measure length horizontally; C and D measure it along the fine blue lines. So there are four different measures: the A-B and C-D distances along a horizontal line, and the A-B and C-D distances along a fine blue line (warning: "distance" here is a slight lie - you have to measure "interval", which is $\sqrt{\Delta x^2-c^2\Delta t^2}$ rather than the Euclidean distance you see on the graph, $\sqrt{\Delta x^2+c^2\Delta t^2}$ - this has the consequence that some lines that are longer on the graph are shorter in reality).

You asked about symmetry. That's why I've drawn D, even though I haven't used that letter yet. I can draw the equivalent graph using the frame where C and D are at rest. It looks like this:

This is a mirror of the first graph - now the blue lines are vertical and the red lines are sloped and closer together. The "same experiment" is A moving from C to D, and the same graphs with horizontal and slanted fine lines (just left-right reversed) can be drawn:

That's the symmetry you were missing. But you need to add D to get it, or in this frame there's nothing for A to move to and you can't do the same experiment as you did with the first frame. If you ignore D for a moment, the only thing you can measure is the time between A and B reaching C - and here you can see that the time between those events as measured by C is shorter than the time measured by A and B, by comparing the vertical distance between the crossings.

I hope that helps. You may need a more thorough intro to Minkowski diagrams if you haven't seen them before, but they really are the easiest way to visualise special relativity.

 

[curiousburke]

I still have to digest this more to fully get it, but thank you for doing this!

 

[curiousburke]

Okay, I think I get most of it. The only thing I'm not fully grasping is the later part of the last, actually second last, paragraph in which you say how to read time from the diagram and from whose perspective that time is. What do I measure on the diagram to say find A and C's proper elapsed times during the experiment?

 

[Ibix]

What do I measure on the diagram to say find A and C's proper elapsed times during the experiment?

For a straight line, measure the vertical distance $\Delta t$ and horizontal distance $\Delta x$ between the endpoints. The "length" squared (properly called the interval) of the line is $\Delta s^2=c^2\Delta t^2-\Delta x^2$. When this is positive the proper time along the line is the square root of it over $c$. When it's zero the line represents something travelling at $c$, and proper time is not defined. When it's negative it represents a spatial distance with a length equal to the square root of the absolute value.

Note that some sources define $\Delta s^2$ with the opposite sign. As long as you don't use both conventions in one calculation, it doesn't matter which you use - just reverse the positive and negative in my paragraph above. Note also that the graphs above use years for time and light years for distance, and using these units $c=1\mathrm{ly/y}$, which simplifies the algebra. It also lets you see the sign of $\Delta s^2$ immediately by seeing if the line has a slope greater than, less than, or equal to 1.

 

[curiousburke]

so, without getting a real number, the longer the line the shorter the interval because of the negative sign?

So, vertical lines are easy, like in the last diagram if I'm interested in C between A and B. Using the same diagram, if I want to know the elapsed time for A or B, when C goes from A to B, is this a line we have on the diagram? Also, while the length of a line will be related to the elapsed time, do we need to include differences in the initial clock time to calculate which clock will have more time between events?

2nd edit: I think I see, in the first diagram, B's elapsed time is the vertical line from t=0 to the crossing point with C. Shorter line than C from A to B, so longer proper time

 

[Ibix]

so, without getting a real number, the longer the line the shorter the interval because of the negative sign?

It's not that simple - lines of equal interval starting at the origin all end on a hyperbola (the upward curving line in @robphy's second diagram above is a unit hyperbola, and all lines from the origin to it have interval 1). A line that goes past a hyperbola will have a larger interval than one that ends on it, but its representation on the diagram will be longer than some lines that end on the hyperbola and shorter than others.

With lines that start at the same place you can probably visualise the hyperbolae and estimate which is longer. In general, you probably have to do some maths.

I think I see, in the first diagram, B's elapsed time is the vertical line from t=0 to the crossing point with C. Shorter line than C from A to B, so longer proper time

Yes - but as above, careful with "longer is shorter" as a general rule. Since the lines have the same $\Delta t$ it works out here, though.

 

[curiousburke]

View attachment 341323



View attachment 341329

Checking if I understand this. I seems you can't read A, B and C's proper times directly off a single diagram, but we can we get the elapsed proper times as C goes from A to B for all three from the vertical lines in two diagrams. So, A and B from the first diagram is ~1.7 and C from the second diagram is ~1.4?

 

[Ibix]

Checking if I understand this. I seems you can't read A, B and C's proper times directly off a single diagram

You can get A and B's proper times directly from the first diagram because $\Delta x=0$, so in this case $\Delta \tau=\Delta t$. Similarly you can get C's from the fourth diagram because $\Delta x'=0$ so C's $\Delta\tau=\Delta t'$. You can't get all three off one diagram without doing a fairly simple bit of maths, no. (Although note that @robphy has a clever graphical method of measuring arbitrary proper times).

So, A and B from the first diagram is ~1.7 and C from the second diagram is ~1.4?

The diagram is draw with the speed of C and D being 0.6c relative to A and B, and with A and B separated by 1ly. So the time A and B measure should be 1.66y, and C should measure 1.33y. So you are pretty close.

 

[curiousburke]

So the time A and B measure should be 1.66y, and C should measure 1.33y. So you are pretty close.

I almost said 1.35, but the added precision seemed unjustified :)

I see this method of getting to the answer shows an asymmetry: a single observer/clock in frame A that is assessed at two points in frame B will have less elapsed time then clocks in frame B. Maybe that interpretation is wrong, it's what I guessed when thinking through the triple paradox, which is the same setup, so I could just be holding on to it.

Unfortunately, now I'm taking a big step backwards (sorry). I think I'm understanding the space-time diagrams, but I'm still not really getting how the asymmetrical setup leads to different elapsed times. If B travels from some initial position to C, the space between them contracts and it takes less time. If C travels to B, the same. How does adding A change anything?

In thinking about the youtube triplets, I convinced myself that B was being required to travel the distance to A in uncontracted space because A and B are in the same frame. This would of course lead to C being younger from either perspective since C travels a contracted distance. However, I don't think that is the case in your spacetime diagram analysis (maybe it wasn't on youtube either), because when A travels from C to D, A experiences less elapsed time (there is symmetry). So what is it about comparing a clock in one frame with two in another that causes an asymmetry in the elapsed time?

Is the synchronization somehow involved, or is that just an arbitrary choice of t=0?

 

[robphy]

Here's a Desmos visualization that reconstructs @Ibix 's spacetime diagram:

robphy-PFreply-resolveSeemingContradictions-CausalDiamonds
https://www.desmos.com/calculator/y5aiiixdvx

You can reposition the two events to find the interval between them,
which is calculated as the square-root of the
area of the causal diamond enclosed by two causally-related events.

With the given graph paper, one small diamond has diagonal with interval (1/3).
The causal diamond of OP has 16 diamond areas.
So, the (diagonal's interval) = (sqrt(16))*(1/3) =4/3.
With O at the origin, one can consider events Z only on the hyperbola of radius (4/3).

 

[PeroK]

Unfortunately, now I'm taking a big step backwards (sorry). I think I'm understanding the space-time diagrams, but I'm still not really getting how the asymmetrical setup leads to different elapsed times. If B travels from some initial position to C, the space between them contracts and it takes less time. If C travels to B, the same. How does adding A change anything?

In thinking about the youtube triplets, I convinced myself that B was being required to travel the distance to A in uncontracted space because A and B are in the same frame. This would of course lead to C being younger from either perspective since C travels a contracted distance. However, I don't think that is the case in your spacetime diagram analysis (maybe it wasn't on youtube either), because when A travels from C to D, A experiences less elapsed time (there is symmetry). So what is it about comparing a clock in one frame with two in another that causes an asymmetry in the elapsed time?

Is the synchronization somehow involved, or is that just an arbitrary choice of t=0?

If you are serious about learning SR, you could try Morin's book. The first chapter is free online:

https://scholar.harvard.edu/david-morin/special-relativity

The amount of time you've spent on this random video could have been spent building a solid foundation for the whole subject.

 

[PeroK]

PS I had a look at that video. It's very insightful, but I suspect the ideas might be too advanced until you've grasped the basics of SR yourself. IMO, Mahesh is spot on with everything he says. Having the radio transmitter in the middle is a great idea. But, there's a lot to digest in that 20-minute video.

So, rather than trying to learn SR from that video, I would knuckle down with Morin's book and use Mahesh's video as a test piece. When you reach the stage that his video is obvious, then you know you've understood SR!

 

[Ibix]

Unfortunately, now I'm taking a big step backwards (sorry). I think I'm understanding the space-time diagrams, but I'm still not really getting how the asymmetrical setup leads to different elapsed times. If B travels from some initial position to C, the space between them contracts and it takes less time. If C travels to B, the same. How does adding A change anything?

Forget about Minkowski spacetime for a minute and just look at the diagrams as pictures. Look at the second one, with the fine red lines marked. The two thick and two thin red lines form a rectangle. One blue line is the diagonal. The length of blue line between the fine red lines is longer than the length of thick red line between the fine lines, because one's a diagonal and the other's an edge.

Now go back to thinking of it as a Minkowski diagram. The elapsed time along the blue line between the fine red lines is shorter than the elapsed time along the thick red line between the fine lines, because one's a diagonal and the other's an edge.

That's why the times are different. It's because you picked the red lines to form the rectangle, so the blue is inevitably the diagonal. The third diagram (with slanted fine blue lines) shows what blue did wrong with intuitive reasoning: there is less elapsed time for the destination red clock during the experiment by blue's definition of "during". But the red clocks are not synchronised like that, and blue forgot to allow for the extra time.

 

[curiousburke]

Thank you again for all the explanation. PeroK, I understand your suggestion that getting a solid foundation might be time better spent, but this two way dialog has been a thousand times more productive than anything i could do on my own.

Ibix, I see now how to read the diagrams, and I woke up this morning realizing how to translate what I was saying yesterday into the spacetime diagram. When we rotate into C's perspective, the distance between A and B decreases at t=0. Given the slope of the non-vertical lines in all diagrams are the same magnitude, this shorter distance in the fourth diagram causes the intersection between B and C to happen sooner (shorter vertical line, C's proper time).

So, is this back to what I was saying? C travels trough contracted space between A and B, while B travels through uncontracted space?

Fundamentally, I won't understand until I know how all these lines on the diagrams are calculated so I should go to Morin I guess ... bite the bullet

 

[curiousburke]

FWIW, Ibix, it's probably very frustrating working with people like me, sorry. I can see a lot of what I'm grasping now you said in your first space-time diagrams post.

 

[curiousburke]

So, is this back to what I was saying? C travels trough contracted space between A and B, while B travels through uncontracted space?

maybe I can ask this more clearly. Is the presence of A creating an absolute rest frame in the problem setup? If we didn't have A, how would we know whether B sees the distance to C contracted or C sees the distance to B contracted? Or, would they both see it as contracted and agree on the distance between them, thus eliminating the difference in proper time?

It looks to me that the contraction of distance in the rotation between frames is caused by our choice of x-origin around which we rotate.

 

[PeroK]

FWIW, Ibix, it's probably very frustrating working with people like me, sorry. I can see a lot of what I'm grasping now you said in your first space-time diagrams post.

Probably most of us on here don't believe that you can really understand SR without understanding the mathematics. You're chasing a shadow now. For example, you might be able to follow the world chess championships up to a certain level without knowing the game. There comes a point, however, when any deeper understanding is only possible if you really learn to play the game.

I don't believe the comments on that video from the people who claim they understand it now. If I gave them all a variation on the problem, their understanding would vanish. All they have is an illusion of understanding.

Your difficulties here, IMO, don't stem from any inherent deficiencies on your part, but from trying to understand SR from one video and without the mathematics. If you do look at Morin, you'll find that he goes much more slowly than Mahesh. And, makes you do problems yourself.

We all learn differently, but in my case the intuitive understanding and the mathematics go together.

 

[curiousburke]

I don't believe the comments on that video from the people who claim they understand it now. If I gave them all a variation on the problem, their understanding would vanish. All they have is an illusion of understanding.

I can say with 100% certainty that this is true for at least one of those posters. I still think he has the best explanations of the twin paradox on youtube. Also, while I think the asymmetry in the triplet paradox is a property of problem setup, that is generally the problem setup for the twin experiment.

I do think this exploration, although not as rigorous as learning the math, is improving my understanding. At least it is rapidly pushing the questions that I'm asking. Like now I'm asking: what does it mean to rotate around A @ t=0, x=0 versus around B @ t=0, x=1?

 

[PeroK]

I still think he has the best explanations of the twin paradox on youtube.

If I were teaching a course on SR, then the twin paradox wouldn't appear! Except as an appendix. In fact, that's what Helliwell does in the book from which I learned SR (ten years ago!).

Helliwell's approach is effectively:

1) Learn SR.
2) Resolve the twin paradox.

You are doing the opposite and, inevitably, coming to grief!

 

[curiousburke]

You are doing the opposite and, inevitably, coming to grief!

To be fair, I did learn SR as an undergrad 30 years ago, or maybe I didn't, but I was supposed to. Maybe physics professors should stop handing out 'A's like candy!

 

[robphy]

Look up Minkowski diagrams. I can draw one for this scenario later. I find them very helpful - essentially the answer is that when two frames say they are measuring "distance" they are measuring different lines in spacetime, and there end up being four different things being measured when you say "they measure the distance between them". There would only be a contradiction if they were measuring one or two things.

Because of things like that, a spacetime diagram can be a very helpful tool in both organizing your thoughts and communicating them to others.

As I like to say, "A spacetime diagram is worth a thousand words".
Since it's a map of all of the events of the situation and
since the Minkowski spacetime-geometry encodes all of the relevant physical relationships,
it can (and probably should) be used along with any explanation that someone might give.
Some folks will emphasize one set features in their explanation,
others may emphasize a different set of features...
but the spacetime diagram should be able to support all explanations
and probably help you connect two different explanations.

 

[PeroK]

As I like to say, "A spacetime diagram is worth a thousand words".
Since it's a map of all of the events of the situation and
since the Minkowski spacetime-geometry encodes all of the relevant physical relationships,
it can (and probably should) be used along with any explanation that someone might give.
Some folks will emphasize one set features in their explanation,
others may emphasize a different set of features...
but the spacetime diagram should be able to support all explanations
and probably help you connect two different explanations.

That's about 100 words. Let's see expressed that in a diagram!

 

[cianfa72]

The relative velocity is what makes C and B interpret "now" differently. The spatial separation does not affect that, as should be obvious from the fact that A, who is not spatially separated from C at the event where they meet, also interprets "now" differently from C (but the same as B, who is spatially separated from A).

I'm late for the OP question, but note that observers A and B, supposed to be at rest in the same inertial frame, share the same "now" sets in spacetime.

 

[PeterDonis]

note that observers A and B, supposed to be at rest in the same inertial frame, share the same "now" sets in spacetime

As I said in the parenthetical note in the last part of what you quoted from my post.

 

[curiousburke]

I'm late for the OP question, but note that observers A and B, supposed to be at rest in the same inertial frame, share the same "now" sets in spacetime.

I am assuming this is in response to one of my latest posts about the distance between A and B in figure 1 (A, B perspective) and the distance between A and B in figure 4 (C's perspective), but I don't think I said the spatial separation effected their "now". Does something I said make that indirectly true?

 

[PeterDonis]

I don't think I said the spatial separation effected their "now".

See my post #16, which @cianfa72 quoted, and which was in response to a statement of yours (quoted in that post) that included "spatial separation".

 

[curiousburke]

See my post #16, which @cianfa72 quoted, and which was in response to a statement of yours (quoted in that post) that included "spatial separation".

Okay, I know I had said that near the beginning.

 

[robphy]

Here are a few spacetime diagrams. If you haven't come across them, they're simply plots of the position of an object over time, the custom being that time goes up the page. So a vertical line represents an object that isn't moving, and a line slanted to the left indicates one moving to the left. You may have come across these (usually with time horizontally) as "displacement-time graphs" in high school physics. We take them a little more seriously in relativity, since spacetime is a thing - these are maps of spacetime, and the lines are the 4d objects inhabiting it. You see one 3d slice at a time.

So here's your scenario, with my extra "D" observer. A and B are marked in red and are stationary, C and D are marked in blue and moving to the right.
View attachment 341321
Note that, in this frame, C and D are closer together than A and B - the horizontal distance between the lines ("the space between them") is shorter.

We could mark on the diagram the start and end of the experiment - when C passes A and then B. Let's do that with fine red lines:

[snip]

Here's @Ibix 's spacetime diagram supplemented with "light-clock diamonds"
to help visualize the ticks along segments in spacetime.

An inertial observer's light-clock diamond
has a timelike diagonal parallel to his worldline
and spacelike diagonal Minkowski-perpendicular to his worldline.
Thus the spacelike diagonal is simultaneous according to that inertial observer.
All light-clock diamonds
have lightlike edges (speed of light postulate: eigenvectors of a boost on this plane)
and have equal area (determinant of boost equals 1).

The scale is (1 on @Ibix 's scale)=(3 ticks).
Using @Ibix's labeling of worldlines,
B along x=1 is 3 red-spaceticks [red-"sticks"] away from A and
D is -3 blue-"sticks" from C.

• The undecorated parallel worldlines 5 ticks away from A and C
  help in counting diamonds to set up proportions (via similar triangles)
  when trying to count diamonds involving B and D.
  For instance:
  for v=(3/5)=(6/10)=$\frac{(PQ)}{(OP)}$, we have $\gamma$=(5/4) and k=2.
  
  Length contraction:
  A rod of proper-length 5 [red-]sticks carried by A
  is measured to be 4 [blue-]sticks according to C since $5/\gamma=4$. $(OM)=\frac{(OL)}{\gamma}$)
  A rod of proper-length 5 [blue-]sticks carried by C
  is measured to be 4 [blue-]sticks according to A since $5/\gamma=4$.
  
  So,
  A rod of proper-length 3 [red-]sticks carried by A [whose far end is traced out by B]
  is measured to be 2.4 [blue-]sticks according to C since $3/\gamma=3/(5/4)=(12/5) {\rm\ sticks}=(12/5) (1/3 {\rm\ Ibix})= (4/5 {\rm\ Ibix})$.
  ...and similarly for the rod carried by C [whose far end is traced out by D].

 

[curiousburke]

robphy, you're stuff is next level. One careful read, and I understand maybe 50%. Just another infinity-1 reads and I'll fully get it :)

Seeing you add features to this spacetime diagram gave me an idea. Just to make things more complicated, what about adding a 3rd dimension to represent the perspective? Basically, spacetime diagrams are slices through a block of any possible rotation.

 

[robphy]

robphy, you're stuff is next level. One careful read, and I understand maybe 50%. Just another infinity-1 reads and I'll fully get it :)

Seeing you add features to this spacetime diagram gave me an idea. Just to make things more complicated, what about adding a 3rd dimension to represent the perspective? Basically, spacetime diagrams are slices through a block of any possible rotation.

Thanks.
These approaches come from various attempts (some successful , some less-successful)
to convey the ideas of relativity and spacetime-geometry.

The light-clock diamonds are traced out by the light-signals in light-clocks.
They are already there, implicitly, in the spacetime diagram.
I highlighted them because they lead to this way of calculating by counting areas.

It's not clear what to "add" in a third dimension. There may be something... but I'm not sure.
One should take care to find representations that faithfully represent the physics.

 

[curiousburke]

It's not clear what to "add" in a third dimension. There may be something... but I'm not sure.
One should take care to find representations that faithfully represent the physics.

I thought the same thing, so left it ambiguous figuring you would know :)

I'm thinking two different things, one is the velocity of a third frame from which the other two are measured, so 3d could smoothly transition from one frames perspective to the other.

Second, I'm still trying to conceptualize what it means, but hand wavey, it's the choice of x=0 relative to the observers.

 

[robphy]

I thought the same thing, so left it ambiguous figuring you would know :)

I'm thinking two different things, one is the velocity of a third frame from which the other two are measured, so 3d could smoothly transition from one frames perspective to the other.

Second, I'm still trying to conceptualize what it means, but hand wavey, it's the choice of x=0 relative to the observers.

Here's the original diagram, followed by its boosted version.

If you look at these a little bit and learn how to interpret the geometry and physics encoded,
I think that you can see that they convey the same information...
(...Like a rotated photo has the same information as the original photo.)
by counting ticks and sticks.... and by interpreting the diagonals
of an inertial observer's light-clock diamonds as defining
"at the same place" and "at the same time" for that observer.

So, the second diagram isn't necessary... and, in fact, can be constructed by hand from the first diagram.
(Using v=(3/5)c or (4/5)c [or more generally velocities with a rational Doppler factor]
makes this easy to construct by hand on rotated graph paper.)

 

[robphy]

I still think he has the best explanations of the twin paradox on youtube.

Here's my clock-effect/twin-paradox spacetime diagram using the rotated graph paper.

This is for $\gamma=2$ [so, $v=\sqrt{3}/2$] (the video's situation),
which isn't ideal for handdrawing on rotated graph paper
since $k=2+\sqrt{3}$ (not rational).... so the piecewise-inertial traveler's diamonds don't fall nicely on the rotated graph paper.
I've drawn in the lines of simultaneity, which are parallel to the spacelike diagonal of the traveler's diamonds.
Note $2.5=\frac{10}{\gamma^2}$

With $v=4/5$, we have $\gamma=5/3$ and $k=3$.
Note $3.6=\frac{10}{\gamma^2}=10\left(\frac{3}{5}\right)^2$