Homework Help Overview
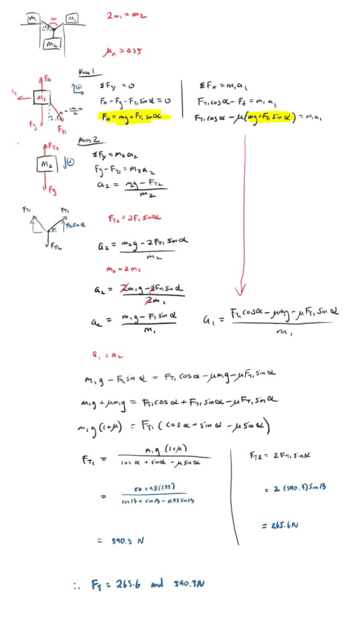
The discussion revolves around a non-equilibrium pulley system involving a specific angle of 154 degrees. Participants are exploring the dynamics of tension in the system and the relationships between the components involved.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Problem interpretation
Approaches and Questions Raised
- Participants are questioning the assumption of equal accelerations in the system and discussing the relationships between the positions of the masses and the geometry of the setup. Some are considering the implications of fixed lengths of the ropes and drawing parallels to related rates problems.
Discussion Status
The discussion is active, with participants offering insights into the relationships between the variables involved. There is a mix of interpretations regarding the nature of tension and its behavior as the angle changes, but no consensus has been reached on the specifics of the calculations or assumptions.
Contextual Notes
Participants note that the problem is framed by a teacher's prompt, emphasizing the non-equilibrium nature of the system. There are discussions about the minimum tension required and the implications of the system's geometry.