Defining equilibrium and movement in pulley arrangements

[Physicsterian]

Homework Statement

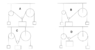
I had to answer which of the pulley arrangements illustrated (see picture) is in equilibrium (the drawing went a bit difficult, please see all outer boxes as equal in size and the middle ones as well) I managed to answer that it is arrangement C, by finding out that equilibrium seems to be the case when the angle between the middle pulley and the rope on each side of it is symmetrical. However, now I want to know the exact physics behind it. Below, I already described my assumptions about it and am wondering if I have concluded it correctly. Plus, I get stuck at how slightly different pulley arrangements will effect equilibrium and movement of the weights. Please, see below, for more details.

Homework Equations

Possibly: Torque (F*R)

The Attempt at a Solution

I assume that C is the one that is in equilibrium, because there the outer weights must be equal in size since the angle that the rope makes with the middle pulley is equally at each side; in other words symmetrical. Looking at the other arrangements, the angle that the rope makes with the middle pulley is asymmetrical. In order to get the middle pulley hanging asymmetrically, the outer boxes must be different in weight. Do I get it right that if the weight hangs more toward the left side, the left weight must be heavier (picture B), and that if the that same weight is hanging even higher, the left weight must be much heavier (picture D)? In the case of arrangement A, the box at the right must be heavier. Am I right in saying that I should not get confused and think there is equilibrium just because the rope won’t move in any of the arrangements. It seems to me that equilibrium is just the case when the weights are equal in size and the weight in the middle is hanging at symmetrical angles in respect to the rope when the pivot points of the outermost pulleys are at the same height.

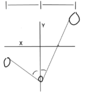
Now, there are four other scenarios at which I get stuck understanding what the arrangement will look like, and in which direction the weight will possibly move:
1) a height difference between the outer pulleys with the same amount of weight hanging at the outermost pulleys
2) a height difference between the outer pulleys with a different amount of weight hanging at the outermost pulleys
3) much radius difference between the outermost pulleys while having the same amount of weight hanging at the outermost pulleys
4) much radius difference between the outermost pulleys while having a different amount of weight hanging at the outermost pulleys
Please, see picture two for the illustration of those arrangements.

It appears to me that the theory behind how those arrangements will look and in which direction possible movement will be, must be all about Torque and that pulley radius and difference in height between the outer pulleys must play a role. However, I do not understand in which way the rules of torque can be applied here, and thus would like to get assistance in figuring out how.

 

[Doc Al]

Just study the middle pulley. What can you say about the tension in the rope on each side of that pulley? What does that allow you to conclude?

 

[Physicsterian]

Just study the middle pulley. What can you say about the tension in the rope on each side of that pulley? What does that allow you to conclude?

Thank you for providing directions. I was having some difficulties with defining what terms I had to search on (as I am fairly new to physics).
At the moment, I am searching on "static pulley equilibrium" and I think that must help me out. Do you think I am on the right way? Do you have additional search terms you can advise me to search on?

Thanks in advance.

 

[Doc Al]

What I'd like you to do is attempt to answer the questions I posed.

What textbook are you using?

 

[Physicsterian]

What I'd like you to do is attempt to answer the questions I posed.

What textbook are you using?

The magnitude of the tension force in the rope must be equal on each side, thus, it seems to me that each outer weight is equal in magnitude to the tension force in the rope at each side. However, since the middle pulley is not making a symmetric angle with the rope at each side, and because it is hanging freely (not connected with a rod to the other pulleys), I doubt if I am concluding it correctly.

The exam I am preparing for has a computer-based learning center, which I have finished. On top of that, I have finished some basic physics books. The library where I get my books from doesn't have intermediate books above that level. There is only one, for my current background, difficult being book, which I am using at the moment, called Engineering Mechanics: Statics, 13th edition, Russel Hibbeler. I combine this with learning via youtube and google.

 

[Doc Al]

The magnitude of the tension force in the rope must be equal on each side

Exactly!

However, since the middle pulley is not making a symmetric angle with the rope at each side

Ask yourself if that's possible, given the fact that the tension is the same on both sides.

 

[Physicsterian]

Ask yourself if that's possible, given the fact that the tension is the same on both sides.

• When the radii of the outer pulleys are the same and they are at the same height, I am quite sure that the angles must be and will stay symmetric, till the angle eventually becomes zero when the weight is lifted up totally.

• When one of the outer pulleys is installed at a higher height and the magnitude of the outer weights is thereby equal, I expect that the middle pulley will balance at the middle of the horizontal distance between the two outer pulleys (x = 0) (option A in my illustration), due to the gravitational force. Therefore, it seems to me that the angles will be asymmetric throughout, even when the outer weights are equal (when equilibrium is the case) It appears to me that when the magnitude of one of the outer weights gets larger than the other, the middle pulley would be pulled up more, while still maintaining its horizontal position at x = 0. This, again, because of the gravity force, trying to balance the freely moveable pulley with the weight attached to it, toward the middle. Hence, this would get the middle pulley make an asymmetric angle when the pulleys are installed at a different height.

On the whole, for freely moveable pulleys, symmetric angles only seem possible to me if the attachment height of both outer pulleys are equal. In cases where there is a difference in attachment height, I think, the angle won't be symmetric ever due to the gravity. If a freely moveable pulley weren't the case and the weight was for example attached to the rope by a knot, then, I think, asymmetrical angles would even be possible for pulleys attached at the same height.

Am I concluding all of this correctly?

 

[Doc Al]

My only point was a simple one. In your first post you showed four scenarios and had to pick which was in equilibrium. Without looking at anything other than the middle pulley, you can immediately exclude three of the four scenarios from being in equilibrium. (I think you pointed this out yourself.) If the angle that the ropes make with the middle pulley is not symmetric, then there will be a net horizontal force on that pulley (since the tension is the same on both sides).

 

[Physicsterian]

My only point was a simple one. In your first post you showed four scenarios and had to pick which was in equilibrium. Without looking at anything other than the middle pulley, you can immediately exclude three of the four scenarios from being in equilibrium. (I think you pointed this out yourself.) If the angle that the ropes make with the middle pulley is not symmetric, then there will be a net horizontal force on that pulley (since the tension is the same on both sides).

Got it. Thanks for your help.