jim hardy
Science Advisor
Homework Helper
Dearly Missed
- 9,832
- 4,898
The reason i wrote my too-long post the way i did is
when i read this
i tried to re-create his dilemma in my own mind to see from where he is coming.
This i could not follow
" then Vout would have to be 1.996V in order for it to simultanteously be 2V. ? Since the input differential is dependent on the output, what is this equation even saying? "
so i decided 'This fellow needs to go back to his very basics.'
And that's where i tried to take him.
"Inputs are equal" is just a restatement of 'infinite gain' that alleviates the need to deal with the concept of infinity.
I came up from tubes where gain of a hundred in one device is phenomenal and i at first rejected as absurd the notion of infinite gain in something the size of a pencil eraser.. Caused me trouble for some time , using instead 'inputs will be driven equal' got me past that mental stumbling block.
I thought he needed similar help.
I take your point, i could have finished my post by addressing his Avol of only 1000. To me that's the next step, going from the ideal to a real model, and I tend to do one step per post.btw it was your post 8 that prompted me to say this in my post 19 :
old jim
when i read this
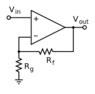
TimNJ said:...but I am struggling with one concept. Say we apply a 1V step input, with an Aol of 1000, and a feedback factor of 0.5 (so ideal closed loop gain of 2), how does the op-amp "know" to stop rising at Vout = 1.996V?
The finite gain equation says Vout = Aol(V+ - V-), but in this case if V+ = 1V, and V- = 0.5(Vout), then Vout would have to be 1.996V in order for it to simultanteously be 2V. ? Since the input differential is dependent on the output, what is this equation even saying?
The op-amp does not "know" you want 2V on the output, per say...so what's stopping it from rising to 1.997V, and producing 1.5V on the output?
i tried to re-create his dilemma in my own mind to see from where he is coming.
This i could not follow
" then Vout would have to be 1.996V in order for it to simultanteously be 2V. ? Since the input differential is dependent on the output, what is this equation even saying? "
so i decided 'This fellow needs to go back to his very basics.'
And that's where i tried to take him.
"Inputs are equal" is just a restatement of 'infinite gain' that alleviates the need to deal with the concept of infinity.
I came up from tubes where gain of a hundred in one device is phenomenal and i at first rejected as absurd the notion of infinite gain in something the size of a pencil eraser.. Caused me trouble for some time , using instead 'inputs will be driven equal' got me past that mental stumbling block.
I thought he needed similar help.
I take your point, i could have finished my post by addressing his Avol of only 1000. To me that's the next step, going from the ideal to a real model, and I tend to do one step per post.btw it was your post 8 that prompted me to say this in my post 19 :
Forget iterations and approach to equilibrium , that's too much math.
old jim
Last edited: