How Does Angle of Incidence Affect Deodorant Dispersion in Physics IA?

[Vishwa Jad]

In about 4 days I have to hand in my final draft for my Physics Internal Assesment and require help in linearising a graph. My research question is : "How do the different angles of incidences (from the vertical) of a roll-on deodorant bottle’s ball that rolls a distance of 20cm on parafilm surface, affect the total liquid mass (g) of the deodorant that is dispersed?"

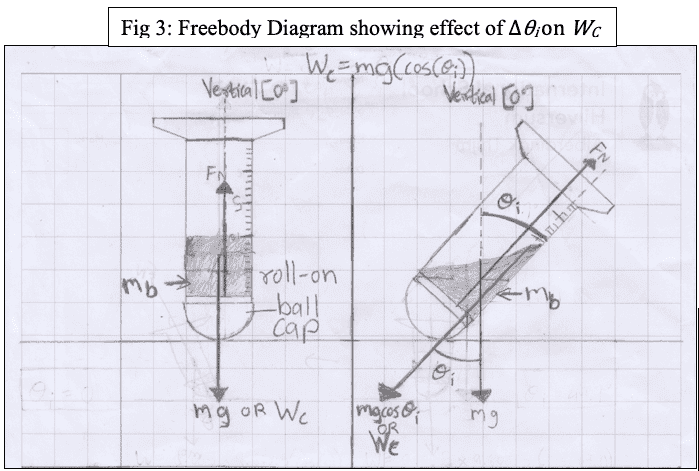
In my initial hypothesis, I had relied on the equation (Wc=mgcos(theta i)), where Wc is the parallel component of the weight force down the bottle and theta i is the incident angle (independent variable). From the cosine graph, as the x (incident angle) is increased, the Wc decreases at a growing rate of decline. If the Wc is decreasing, I had predicted that liquid deodorant dispersion would be less since there would be a smaller force pushing the liquid into the inside of the ballcap, causing them to be dispersed at a slower rate.

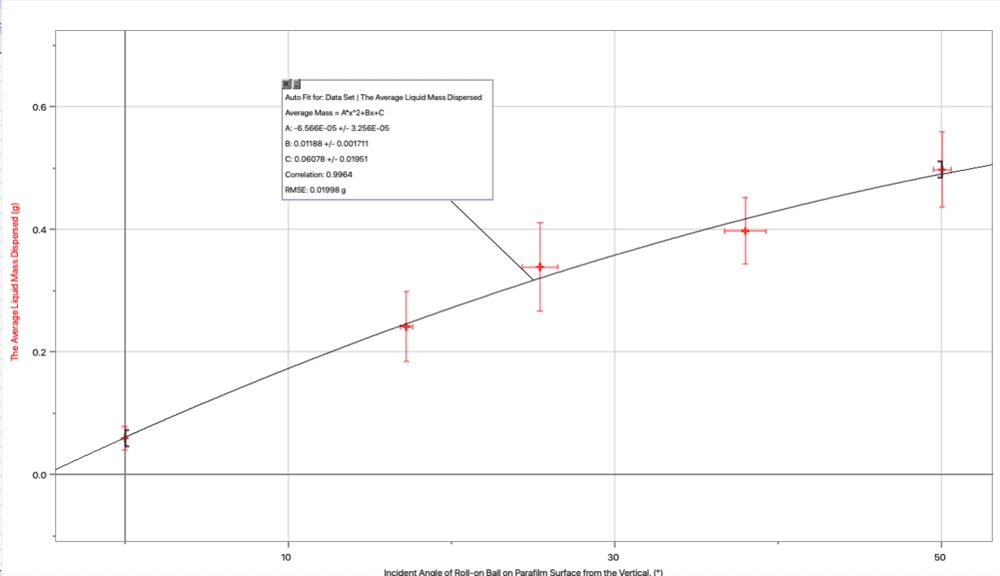
However, according to my results, the opposite happened. Therefore, as the incident angle from the vertical (theta i) was increased, the total liquid mass dispersion increased. Now I think it may have been because I based my hypothesis on the wrong equation and the relevant equation may have been (Wc=mgsin(theta i), which would also explain the results. I just want someone to clarify what equation I am dealing with when trying to find the component of the weight force down the bottle/ parallel to the bottle:

Graph:

 

[kuruman]

This is an interesting experiment. It looks like you assume that the "normal" force on the liquid has something to do with the amount of liquid that is dispensed. Fair enough. However you do not seem to understand that this force is related to hydrostatic pressure which you will have to model. Hydrostatic pressure depends on depth. When the bottle is upright (θ = 0) the pressure or force per unit area is the same at all points where the liquid wets the back of the ball-cap. When the bottle is tilted, at different points on the back of the ball-cap you have different amounts of pressure because these points are at different depths. How the pressure varies with angle depends on the volume of the liquid and the diameter of the bottle which you don't give.

I hope that after each measurement at a given angle you replenished the fluid that was dispensed. Given that this was the case, it would have been interesting to test the pressure hypothesis by keeping the bottle upright and measuring the amount of dispensed liquid as a function of dispensing distance. If the hypothesis is right, then the amount dispensed over 40 cm would be less than twice the amount dispensed over 20 cm. This situation would be easier to model than the one you chose.

It's a pity this post has been left unanswered for 6 months. I think the choice of title and forum didn't help.

 

[anorlunda]

I moved the thread to Other Physics Topics hoping to attract other answers.