How Does Earthing Affect Charge Distribution on Spherical Shells?

[gracy]

I don't understand charge distribution properly.
Here is what I found somewhere
Figure (1)shows three concentric thin spherical shells A,B and C of radii a,b and c respectively.The shells A and C are given charges q and -q respectively and the shell B is earthed.Find the charge appearing on the surfaces of B and C.
Figure (2) shows how charge distribution would take place.

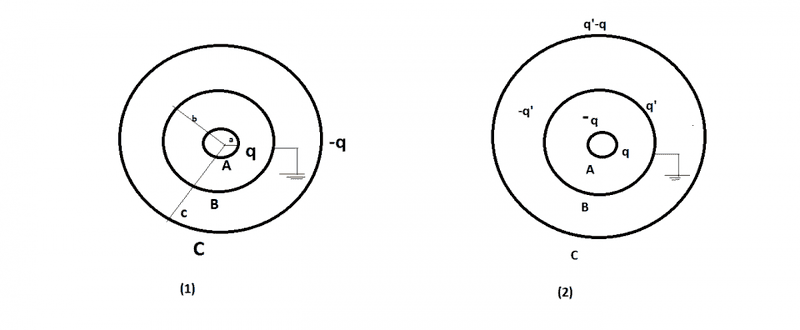
Charge distribution:The inner surface of B must have a charge -q from the Gauss's law.Suppose,the outer surface of B has a charge q'.The inner surface of C must have a charge -q' from the Gauss's law.As the net charge on C must be -q ,it's outer surface should have a charge q'-q.The charge distribution is shown in the figure.But as per my understanding
The inner surface of B must have a charge -q so that net charge becomes zero because as shell B is earthed it has to be at zero potential.But then we will be violating "conservation of charge"law.As originally shell B does not have any charge.That's why the outer surface of B should have charge q.
I am all confused about shell C.As according to Gauss's law it is ok to have charge q on the outer surface(i.e inside shell C) of B because this gives net charge q inside shell C and that was the case initially.But then total charge of shell C becomes zero and that violates "conservation of charge"law.
Please help.I am really Sorry if it is confusing.

 

[gneill]

Shell B is not isolated since it is connected to ground. Ground can be treated like a big neutral sea of available charges (positive or negative). If they can (if there's a conductive path) they will move to try to cancel charges and their fields.

So the charge conservation rule doesn't hold for shell B since it can draw on charges through its ground connection.

Did the problem source determine a value for the charge q' ?

 

[gracy]

How can we determine if any shell is isolated?

 

[gracy]

Did the problem source determine a value for the charge q' ?

No.

 

[gneill]

How can we determine if any shell is isolated?

A body is isolated if it has no external connections that can conduct charges, that is, charges cannot leave or exit the object. Shell B is not isolated because it has a connection to ground by which charges can move onto or off of the shell.

 

[gracy]

the charge conservation rule doesn't hold for shell B

Can charge conservation be applied to shell C,I think yes.Because it seems isolated.

 

[gneill]

Can charge conservation be applied to shell C,I think yes.Because it seems isolated.

Yes. Both shells A and C are isolated so charge conservation holds for them.

 

[gracy]

Suppose,the outer surface of B has a charge q'.The inner surface of C must have a charge -q' from the Gauss's law.As the net charge on C must be -q ,it's outer surface should have a charge q'-q

Please help me to understand this.How and why?Any hint?

 

[gneill]

There can be no electric field inside a conductor, so something must prevent any field originating in the interior of shell C from penetrating shell C's material. If shell B has some charge q' on its surface, then that charge will attract its opposite charge -q' to the inner surface of C, satisfying the requirement of cancelling the field from B. That charge of -q must have come from the total charge q on the C shell (the C shell being isolated), leaving charge q-q' to present at the outer surface of C.

 

[gracy]

There can be no electric field inside a conductor,

But according to @nasu

If you put charge inside, the field does not have to be zero.

 

[gneill]

I believe that @nasu was referring to the field inside the cavity, not inside the shell conductor.

 

[gracy]

I quoted that from other thread
https://www.physicsforums.com/threads/charges-on-inner-and-outer-shell.843840/#post-5296509
see post #6

 

[gracy]

I believe that @nasu was referring to the field inside the cavity, not inside the shell conductor.

Did you mean shell C by shell conductor?

 

[gracy]

I believe that @nasu was referring to the field inside the cavity, not inside the shell conductor.

If there is a charge inside the cavity of a non conducting shell,it is a trivial thing that the field is not zero.
Right?

This is true for conductive shell too.
If you put charge inside, the field does not have to be zero.

But he did not mention cavity anywhere?Did he mean If you put charge inside the cavity of conducting shell,the field does not have to be zero.

 

[gneill]

But he did not mention cavity anywhere?Did he mean If you put charge inside the cavity of conducting shell,the field does not have to be zero.

Yes. If you put a charge in the cavity there will be a field in the cavity due to that charge.

 

[gracy]

Please answer my post #13.

 

[gneill]

Please answer my post #13.

I wanted to distinguish the shell itself from the cavity that the shell surrounds. By shell conductor I mean the conductive material of the shell itself.

 

[gracy]

If any conductive shell surrounds a hollow conductor,can that hollow conductor be treated as a cavity inside the conductive shell?

 

[gracy]

there will be a field in the cavity due to that charge.

But the field would be zero inside the conductor surrounding that cavity?

 

[gneill]

If any conductive shell surrounds a hollow conductor,can that hollow conductor be treated as a cavity inside the conductive shell?

I'm not sure that I understand what you're getting at. As far as I can tell you're describing nested conductive shells, or several hollow objects inside another shell. As you've seen, charges on nested shells can influence the field external to the outer shell. Any fields in the interior of that outer shell will be due to charges in its cavity, and they can interact between each other the way charges usually do. These charges can reside on hollow conductors.

Can you draw a scenario that might make your query more clear??

 

[gneill]

But the field would be zero inside the conductor surrounding that cavity?

Yes. The external field must stop at the surface of any conductor.

 

[gracy]

If any conductive shell surrounds a hollow conductor,can that hollow conductor be treated as a cavity inside the conductive shell?

Can you draw a scenario that might make your query more clear??

What I am asking is, are these two same?

 

[gneill]

Well, the same in what way? In the diagram on the left one could place a charge on the inner conductor and there would be a field surrounding it in the open space between it and the outer shell. In the diagram on the right that space is filled with conductor (it's part of the shell) so there would be no field in that space, and there's no isolated conductor to hold a charge. In effect you have only one shell in the diagram on the right.

 

[gracy]

and there's no isolated conductor to hold a charge.

Then where would the charge go if given ?I am referring to the cavity case.

 

[gracy]

there would be a field surrounding it in the open space between it and the outer shell

But there is not any open space between it and the outer shell as far as I can see.

 

[gneill]

Then where would the charge go if given ?I am referring to the cavity case.

It would migrate through the conductive material to the surface of the shell. This is the basic premise where a charge placed on a conductive spherical shell resides at its surface.

 

[gneill]

But there is not any open space between it and the outer shell as far as I can see.

Perhaps I am misreading your intentions with your diagrams? You don't indicate what's solid material and what is not. I interpreted your cases as follows:

 

[gracy]

In the pictures you drew both inside and outside shells are hollow conductors,right?

 

[gneill]

In the pictures you drew both inside and outside shells are hollow conductors,right?

White is empty space, color is conductor.

 

[gracy]

What I am asking is can that hollow conductor (hollow shell :shell containing cavity inside)be treated as a cavity inside the conductive shell?[/QUOTE]