Yossi33
- 22
- 3
- Homework Statement
- Physical pendulum time period
- Relevant Equations
- T=2pi*(I/mgh)
hello, i have some diffuculties with this problem, there's the point where the spring is attached to the rod and according to the equation of time period of physical pendulum , h represent the distance from the COM and the pivot point. here the pivot point is at the COM. and i know that it can't be (then the T would be infinity). i don't know if i need to calculate the T of the spring and it would be the same but than what part of the mass is attached to it.
thanks for the help.
https://ibb.co/nsGTrQw
[Mentor Note -- Newbie OP reminded to upload images to PF to avoid confusion when externally linked images disappear (and the associated suspicions of student cheating). All associated images have been uploaded by the Mentors]
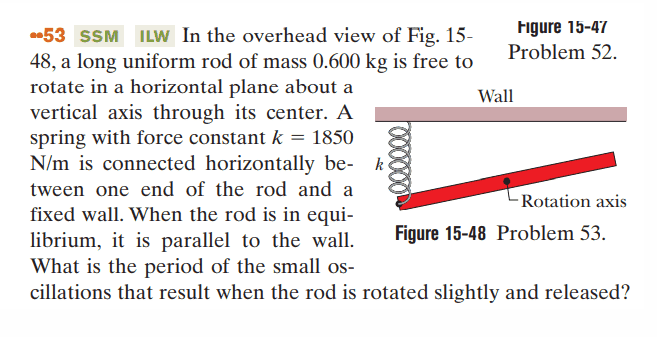
thanks for the help.
https://ibb.co/nsGTrQw
[Mentor Note -- Newbie OP reminded to upload images to PF to avoid confusion when externally linked images disappear (and the associated suspicions of student cheating). All associated images have been uploaded by the Mentors]
Last edited by a moderator: