How does the incline of the rod depend on mass and force F?

[bolzano95]

Homework Statement

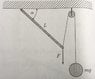
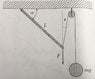
We have a rod with length L and with the left end the rod is fixed to the ceiling in such a way it can swivel. As we can see from the picture (attached file) on right end two forces are acting on the rod: F and mg.
The question is: How does the incline of the rod depend on mass and force F?

Homework Equations

The Attempt at a Solution

I started solving this problem generally. Started to draw force diagram, but got more unknown variables than there are equations. When I looked up to the solution sheet there was written:
FL\cos\alpha = mgL\cos\frac{\alpha}{2} From where did they conclude the angles?
I think from the picture you cannot deduce this yourself. Did they made an assumption that is obvious from the picture but I missed it?

 

[BvU]

Ciao Bolzano,

How does the incline of the rod depend on mass and force F ?

You sure this is the full problem statement ? No mention of equilibrium, for example ?

$FL\cos\alpha$ is the torque around the swivel point from $F$. So the other must be that from the tension in the wire. But where does the $\alpha \over 2$ come from ? Some goniometric relationship we both miss ?

Because: I always like to try things like 'what if F is zero' or 'what if swivel and pulley are further apart ?'

And a $\LaTeX$ tip: use ## \cos\alpha $to get$\ \ \cos\alpha##

 

[bolzano95]

BvU,
Attached picture and the question is everything there is.For the torque this is logical, but for the angles I truly have no idea from where they deduced this connection. Thanks for the tip

 

[haruspex]

Some goniometric relationship we both miss ?

Assuming equilibrium, which is necessary to get anywhere, the balances of vertical and horizontal forces give the angle of the string.

 

[CWatters]

Humm.. I tried summing the torques about the top end of the rod to zero (no angular acceleration) but nearest I got was

FLCos(α) = mgCos(α +β)

where β is the angle the string makes with the vertical. To get the book answer that would mean β = -α/2.

I haven't finished trying to sum the forces to zero but... Both ends of the rod are free to rotate so I think that means the forces at both ends must point along the rod?

 

[BvU]

the balances of vertical and horizontal forces give the angle of the string

I don't see it.. Depending on where the pulley is hanging from the ceiling, the torque from the wire can be a full $mgL$

 

[CWatters]

I think I agree. Here is my working for post #5

Spoiler

Tension in string T = mg
Angle string make with vertical = β

Sum torques about top end of rod.. clockwise +ve..

FLCos(α) - TCos(β)*LCos(α) - TSin(β)*LSin(α) = 0

FLCos(α) - TL{Cos(β)*Cos(α) - Sin(β)*Sin(α)} = 0

Trig Identity..
cos(α)*cos(β) - sin(α)*sin(β) = cos(α + β)
so

FLCos(α) - TLCos(α+β) = 0

FLCos(α) = TLCos(α+β)

T=mg

FLCos(α) = mgCos(α + β)

Close to the book answer but can't seem to eliminate β.

 

[haruspex]

I think I agree. Here is my working for post #5

Spoiler

View attachment 226086

Tension in string T = mg
Angle string make with vertical = β

Sum torques about top end of rod.. clockwise +ve..

FLCos(α) - TCos(β)*LCos(α) - TSin(β)*LSin(α) = 0

FLCos(α) - TL{Cos(β)*Cos(α) - Sin(β)*Sin(α)} = 0

Trig Identity..
cos(α)*cos(β) - sin(α)*sin(β) = cos(α + β)
so

FLCos(α) - TLCos(α+β) = 0

FLCos(α) = TLCos(α+β)

T=mg

FLCos(α) = mgCos(α + β)

Close to the book answer but can't seem to eliminate β.

Yes, I think I was hasty. Need more time to look at this again.

 

[kuruman]

The known answer can be obtained under the following assumptions: (a) the pulley has vanishingly small radius and (b) the distance from the point of support of the rod to the center of the pulley is equal to the length of the rod $L$, that is when $\alpha =0$, the tip of the rod is at the center of the pulley.

 

[haruspex]

The known answer can be obtained under the following assumptions: (a) the pulley has vanishingly small radius and (b) the distance from the point of support of the rod to the center of the pulley is equal to the length of the rod $L$, that is when $\alpha =0$, the tip of the rod is at the center of the pulley.

Yes, I suspected that was the missing information. Thanks - now I don't need to check it.

 

[kuruman]

Yes, I suspected that was the missing information. Thanks - now I don't need to check it.

I appreciate your trust.

 

[BvU]

Measured the drawing on the screen to test that one. Rod was some 10% longer.

 

[CWatters]

Yeah it's looking like a badly set question.

 

[kuruman]

For whatever it's worth, I found an expression for $F/mg$ in the general case where the length of the rod is a fraction $\lambda$ of the distance $D$ between the hinge and the pulley axis ($\lambda=L/D$).
$$\frac{F}{mg}=\frac{\tan\alpha}{\sqrt{1-2\lambda\cos\alpha+\lambda^2}}$$It reduces to the previous expression when $\lambda =1$.

 

[vela]

I think the OP just misread the solution, or there was a typo. The lever arm for the rod's weight is L/2, so the torque about the pivot is $(mgL\cos \alpha)/2$, not $mgL\cos(\alpha/2)$.

 

[BvU]

Hehe, $m$ is the mass that hangs from the pulley, not the mass of the rod.

 

[vela]

I guess I should have read the problem statement. :)

I think the solution is just wrong.

 

[kuruman]

I think the solution is just wrong.

I disagree. Please see posts #9 and #14.